Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
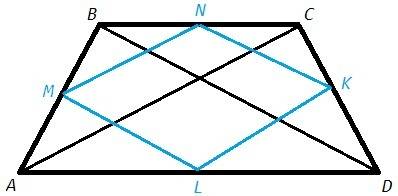
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
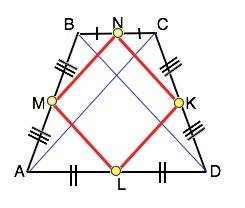
Объясняю о трапеции на фото. Так как углы при основании трапеции равны а половинки сторон, разделенные точками M, N, K, L равны(только половинки каждой стороны равны, а не все вместе равны) ==>> о теореме о равенстве треугольников по углу и двум сторонам треугольники AML и LKD равны, а также треугольники MBN и NCK равны. Так как они равны, значит MN = NK и ML = LK. Так как BH и CH1 высоты, то углы четырехугольника HBCH1 прямые, а значит это прямоугольник. Так как HBCH1 прямоугольник, у прямоугольника противоположные стороны равны и параллельны, то NL перпендикулярно BC и AD. Так как углы BNL = CNL = 90 градусов, углы BNM = CNK, то очевидно что углы MNL = KNL. Аналогично доказывается равенство углов MLN и KLN. Исходя из доказанного равенства углов MLN = KLN и углов MNL = KNL , а также того, что сторона NL общая для треугольников LMN и LKN ==>> LMN = LKN(треугольники), а значит MN = MLи NK = KL, а так как MN = NK и ML = LK по доказанному ==>> все стороны четырехугольника MNKL равны, а значит это ромб.
∠BAC = 55° - вписанный угол равен половине дуги, на которую опирается
⇒ ∪BC = 2*∠BAC = 2*55° = 110°
Дуги AB, AC и BC образуют окружность, значит, в сумме дают 360°
∪AB + ∪AC + ∪BC = 360°
∪AB + 1,5∪AB + 110° = 360°
2,5∪AB = 250°
∪AB = 100°
∪AC = 1,5∪AB = 1,5 * 100° = 150°
∠AOC - центральный, равен дуге, на которую опирается. ⇒
∠AOC = ∪AC = 150°
ответ: ∠AOC = 150°