7 см
Правильное условие:
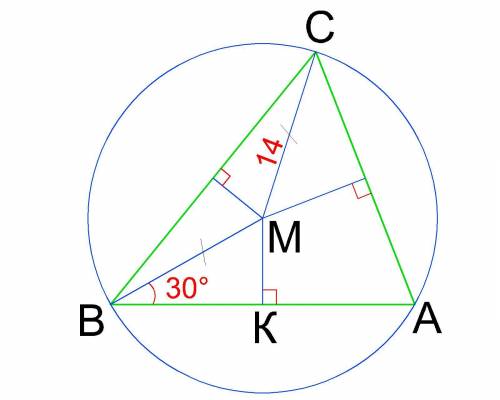
В остроугольном треугольнике ABC серединные перпендикуляры к сторонам BC и AC пересекаются в точке M. Известно, что MC = 14 см, ∠AВМ = 30°. Найдите расстояние от точки M до стороны AB. ответ дайте в сантиметрах.
Объяснение:
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной окружности.
Значит МА=МВ=МС=R = 14 см.
Тогда ΔАМВ - равнобедренный с основанием АВ и ∠МАВ=∠МВА=30°.
Расстоянием от т.М до стороны АВ есть высота равнобедренного ΔАМВ.
Построим высоту МК. Получили прямоугольный ΔВМК с прямым ∠МКВ и гипотенузой МВ.
Катет МК = sin∠MВK * MВ.
Т.к. ∠МВК = ∠АВМ = 30° и МА = 14 см, то
МК = sin 30° * 14 = 7 (см)
7 см
Правильное условие:
В остроугольном треугольнике ABC серединные перпендикуляры к сторонам BC и AC пересекаются в точке M. Известно, что MC = 14 см, ∠AВМ = 30°. Найдите расстояние от точки M до стороны AB. ответ дайте в сантиметрах.
Объяснение:
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной окружности.
Значит МА=МВ=МС=R = 14 см.
Тогда ΔАМВ - равнобедренный с основанием АВ и ∠МАВ=∠МВА=30°.
Расстоянием от т.М до стороны АВ есть высота равнобедренного ΔАМВ.
Построим высоту МК. Получили прямоугольный ΔВМК с прямым ∠МКВ и гипотенузой МВ.
Катет МК = sin∠MВK * MВ.
Т.к. ∠МВК = ∠АВМ = 30° и МА = 14 см, то
МК = sin 30° * 14 = 7 (см)

Подставим: 16 =
2S = 96*16
2S=1536
S=768
ответ: 768