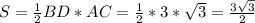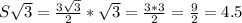Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
АО = ОС = АС/2
BO = OD = BD/2
Диагонали разбивают ромб на 4 равных прямоугольных треугольника. Из любого треугольника по теореме Пифагора находим сторону:
1) АС = 8 см, BD = 6 см.
АО = 8/2 = 4 см, ВО = 6/2 = 3 см
а = √(АО² + ВО²) = √(4² + 3²) = √(16 + 9) = √25 = 5 см
2) АС = 16 см, BD = 12 см,
АО = 16/2 = 8 см, ВО = 12/2 = 6 см.
а = √(АО² + ВО²) = √(8² + 6²) = √(64 + 36) = √100 = 10 см
3) АС = 2,4 см, BD = 1 см.
АО = 2,4/2 = 1,2 см, ВО = 1/2 = 0,5 см
а = √(АО² + ВО²) = √(1,2² + 0,5²) = √(1,44 + 0,25) = √1,69 = 1,3 см