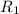 -радиус меньшей окружности
-радиус меньшей окружности
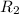 -радиус большей окружности
-радиус большей окружности
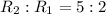
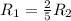
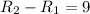
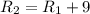
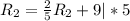
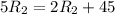
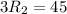
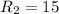 (см)-радиус большей окружности
(см)-радиус большей окружности
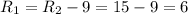 (см)-радиус меньшей окружности
(см)-радиус меньшей окружности
Равнобедренный треугольник АВС, АК - медиана на ВС
Проводим медиану ВМ на АС = высота, биссектриса.
Точка пересичения медиан = О
Медианы пересекаются в треугольнике и делятся в отношении 2 :1 начиная с вершины.
АК = 6 см, что составляет 3 части АО= 2 частям = 4 см, ОК= 1 части = 2 см
Треугольник АОМ -
ОМ = АО х sin угла ОАМ = 4 х sin 15= 4 х 0,2588=1,0 = 1 часть медианы, высоты ВМ
АМ = АО х cos угла ОАМ = 4 x cos 15 = 4 х 0,9659 = 3,9
АС = 2 х АМ = 7,8
Площадь = 1/2 АС х ВМ
ВМ = 3 х ОМ = 3см
Площадь = 1/2 7,8 х 3 = 11,7
В прямоугольном треугольнике, образованным апофемой боковой грани и высотой пирамиды, апофема гипотенуза , а угол при вершине = 30 град.
Напротив него лежит катет = 1/2 гипотенузы = 4/2=2 см
Этот катет является частью медианы (высоты, биссектрисы) трееугольника основания и он раве 1/3 все медианы, т.к. в точке пересиченя медианы деляться в отношении 2:1 начиная с вершины. В правильном треугольнике центром треугольника является точка пересичения высот (медиан..).
Значит вся высота = 2 х 3 = 6 см.
В трееугольнике основания углы = по 60 град.
Сторона треугольника = гипотенузе прямоугольногро треугольника основания = высота (катет) : sin a = 6 : (корень 3/2) = 4 х корень3
Площадь основания = 1/2 х сторона треугольника х высоту = 1/2 х 4 х корень3 х 6 =
= 12 х корень 3
Периметр треугольника = 4 х корень3 х 3 = 12 корень3
Площади боковых граней = 1/2 периметр основания х апофему = 1/2 х 12 корень3 х 4 =
=24 корень 3
Общая площадь = площадь осннования + площадь боковой поверхности= 12 х корень 3 + 24 корень 3 = 36 корень3