1. 50
2. гипатенуза 10
площадь 24
3. Р=
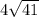
S= 40
4. S= 13,5
Объяснение:
1. 5 * 5*2 = 50
2. 6^2 + 8^2 = 100
находим корень 100, получается 10.
площадь 6*8:2=24
3. 5^2 + 4 ^2 = 41
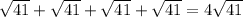
Это был периметр.
S=5*4*2=40
4.
Делим трапецию на треугольник и квадрат.
Треугольник равнобедренный так как там два одинаковых угла(45° и 45°) и один угол 90°
Отсюда СН=НК
А отсюда, как дано в условии АН=НК=СН(высота)=ВН=ВС=ВА(высота)
Находим СН.
По Пифагору. Зная, что СН=НК
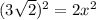
Так х=3
Теперь находим площадь квадрата и треугольника, а после сложить.
3^2 + 3^2:2= 9+4,5=13,5
Теперь мы рассмотрим треугольник МОТ. У него МО = 5 см, и угол МОТ = 120 градусов. Следовательно, по теореме синусов мы можем найти сторону МТ.
МТ/(sin MOT) = 2R
MT/
MT = 10*
Для вычисления площади нам нужна третья сторона. Треугольник MTS - прямоугольный, а значит, мы можем применить теорему Пифагора:
х = 5.
Теперь мы можем найти его площадь по половине произведения его катетов.
2) Расстояние от точки до прямой - перпендикуляр, опущенный из этой точки на прямую.
Точка из т.Т на прямой MS допустим, называется, К.
Итак, мы имеем прямоугольный треугольник МТК.
Но перед тем, как к нему переходить, рассмотрим другой треугольник, треугольник OTS. Он равносторонний (OS=5(радиус окружности), TS=5(мы нашли по теореме Пифагора), OT = 5 (радиус окружности)). А значит, угол OST = 60 градусов.
Угол М теперь находится просто: 180 - 90(это угол MTS) - 60 (это угол OST) = 30 градусов.
Вернемся к треугольнику MTK, в котором MT =
А катет, лежащий против угла в 30 градусов равен половине гипотенузы.
Следовательно, искомое расстояние от точки Т до прямой MS =