Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
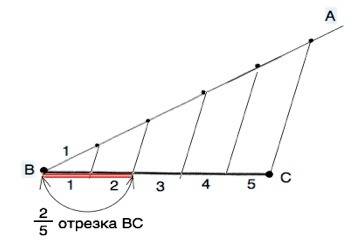
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
а)продолжим КС1 до точки Т, треугольники В1С1К и С1ТЕ равны, значит ТЕ=1
прямы KS и BD1 параллельны, В1К=1, значит SD1=3
проведём прямую TN проходящую через S
NO-SD1=SD1-TE=2
значит NO=5
треугольники NPO и PB1K подобны по 3 углам
NO/B1K=OP/PB1=5/1
OP=5x
PB1=x
OB1=6x
значит ОА1=3х
А1Р=2х
А1Р/PB1=2/1
б)опустим перпендикуляр из В1 на линию пересечения плоскостей КС1
КС1²=В1К²+В1С1²
КС1=√17
треугольники В1С1М и В1С1К подобны по трём углам
КС1/В1С1=КВ/B1M
(√17)/4=1/B1M
B1M=4/√17
PB1- перпендикуляр к плоскости В1С1СВ
PB1=4/3
угол РМВ1 - угол между плоскостями которые даны
tg(PMB1)=PB1/MB1=(4/3)/(4/√17)=(√17)/3