Втреугольнике efp ef = ep, fp= 1,5 ef. периметр треугольника efp равняется 7 см. найдите сторону ep.

👇

Ответ:

russalinagaras

09.11.2020

Т.к. Р=a+b+c (сумма всех его сторон) и еще т.к. EF=EP, то
P=EF+EF+1,5EF
7=3,*5EF, отсюда будет, что
EF= 2
FP = 1,5*EF = 1,5*2 = 3
ответ: 3

4,6(63 оценок)

Открыть все ответы

Ответ:

alexssrus1

09.11.2020

1. Прямая ВC формула прямой у=(3-х)/7

Прямая АВ формула прямой у=2х-21

Прямая АС формула прямой у= -х-3

2. у=9-3х медиана АА1

у=1/3х-39/9 - медиана ВВ1

у= -0,5х-1 - медиана СС1

3. у(АА2)=7,1х-51,5

ВВ2 высота у=х-11

СС2 уравнение у= -0,5х-1

4. А3(5;-6) т пересечения медианы АА1 и высоты ВВ2

5.tg∠A=3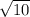 $\sqrt{10}$

tg∠B=tg∠A

tg∠C=2/3/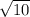 $\sqrt{10}$

Объяснение:

1. Коэфициент при х - это (у-уо)/х т.В(10;-1)

для ВС (у-уо)/х=(-1+21)/10=2

2. АА1 - медиана Определим координаты А1(3; 0)

уравнение медианы АА1

у=9-3х

ВВ1 - медиана В1(1; -4)

у=1/3х-39/9

СС1 С1 (8; -5)

у= -0,5х-1

3.АА2 высота

А2 (7,2; -0,6)

у(АА2)=8,5/1,2х-61,8/1,2=7,1х-51,5

ВВ2 высота

координата В2=(4; -7)

у=х-11

СС2 тС2=С1 (8; -5)

у= -0,5х-1

5. tg∠A=CC1/AC1

Определяем модули векторов СС1 (12;-6) и АС1 (2;4)

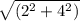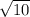
tg∠A= $\sqrt{(12^2+(-6)^2}$ / $\sqrt{(2^2+4^2)}$ =3 $\sqrt{10}$

tg∠B=tg∠A

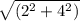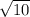
tg∠C=2*AC1/CC1=2* $\sqrt{(2^2+4^2)}$ / $\sqrt{(12^2+(-6)^2}$ =2/3/ $\sqrt{10}$

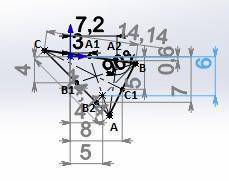
Даны координаты вершин треугольника (6;-9) (10;-1) (-4;1) . Найти: 1. Уравнения прямы. проходящих че

4,8(23 оценок)

Ответ:

Anastasiya6565

09.11.2020

А) Пусть SO высота пирамиды, а KH — перпендикуляр, проведенный из K к плоскости ABC. Очевидно, что основание перпендикуляра H — проекция точки K, лежит на BO — проекции BS. Докажем, что M, H и С лежат на одной прямой. Пусть MC пересекает BO в точке T, и пусть N — середина AB. Запишем теорему Менелая для треугольника BNO и прямой CM: дробь, числитель — BM, знаменатель — MN умножить на дробь, числитель — NC, знаменатель — CO умножить на дробь, числитель — OT, знаменатель — TB = 1, тогда дробь, числитель — 2, знаменатель — 7 умножить на дробь, числитель — 3, знаменатель — 2 умножить на дробь, числитель — OT, знаменатель — TB = 1. Из последнего соотношения получаем: OT : TB = 7 : 3. Но OH : HB = SK : KB = 7 : 3. Значит, точки H и T совпадают. Следовательно, CM пересекает BO в точке H. Плоскость KMC содержит KH, которая перпендикулярна ABC, таким образом, плоскости KMC и ABC перпендикулярны. Поэтому плоскость α проходит через точку C.
б) Заметим, что
KH= дробь, числитель — 3, знаменатель — 10 SO= дробь, числитель — 3, знаменатель — 10 корень из { SA в степени 2 минус AO в степени 2 }= дробь, числитель — 6, знаменатель — 5 .

Вычислим CM при теоремы косинусов:
CM в степени 2 =9 в степени 2 плюс 1 в степени 2 минус 2 умножить на 9 умножить на 1 умножить на косинус 60 в степени circ = 73.
Поэтому площадь треугольника CKM равна
S= дробь, числитель — 1, знаменатель — 2 умножить на дробь, числитель — 6, знаменатель — 5 умножить на корень из { 73}= дробь, числитель — 6 корень из { 73}, знаменатель — 10 .
ответ: б) дробь, числитель — 6 корень из { 73}, знаменатель — 10 .

4,8(34 оценок)

Это интересно:

Образование-и-коммуникации

18.11.2021

Как правильно раскладывать числа: краткое руководство для начинающих...

Кулинария-и-гостеприимство

11.05.2021

Простой и вкусный рецепт шоколадных конфет без лишнего хлопота...

Кулинария-и-гостеприимство

17.08.2021

Как заказать кофе в Макдональдсе: простое руководство для настоящих любителей кофе...

Компьютеры-и-электроника