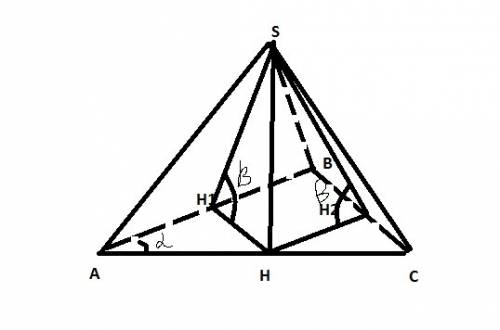
В трапеции АВСD стороны AB=BC=CD, следовательно, трапеция АВСD- равнобедренная.
Проведем СМ параллельно АВ. Противоположные стороны четырехугольника АВСМ параллельны. ABCD – параллелограмм. ⇒ СМ=АВ=СD. Т.к. АD=2 ВС, CМ=МD и СМ=СD. Поэтому треугольник СМD- равносторонний, ⇒ ∠СDM=60°. По свойству внутренних односторонних углов при параллельных ВС||AD и секущей СD ∠ВСD=180°-60°=120°. В равнобедренной трапеции углы при боковых сторонах равны. ⇒ ∠А=∠D=60°, ∠B=∠C=120°
–––––––––––––
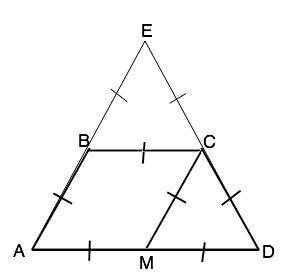
Вариант решения: можно продолжить боковые стороны трапеции до их пересечения в точке Е. Тогда ВС - средняя линия ∆ АЕD, и АЕ=DE=AD. ∆ AED - равносторонний, ⇒ ∠A=∠D=60°, а ∠B=∠C=120°
OM - перпендикуляр к плоскости
MB - наклонная
BO - проекция наклонной ЬИ
AB=5
BD=a√2 (см)
BD=5√2 (см)
BO=1/2BD=