В объяснении.
Объяснение:
1. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+3х+4х = 360° => х = 36°.
Больший угол равен 4х = 144°.
2. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+2х+4х = 360° => х = 40°.
Меньший угол равен 4х = 40°.
3. Площадь квадрата равна площади прямоугольника: 4*9 = 36 =>
Сторона квадрата равна √36 = 6 ед.
4. Площадь прямоугольника равна х*(х+2) = 24. Тогда
х² + 2х - 24 = 0. Решаем квадратное уравнение. => x = 6. (второй корень отрицательный)
Тогда большая сторона равна 6 + 2 = 8 ед.
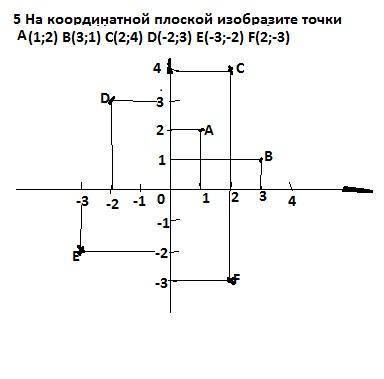
5. Смотри рисунок.
6. Уравнение окружности:
(Х - Хц)² + (Y-Yц)² = R² Тогда
а) Координаты центра: Ц(-5;2) Радиус = 4 ед.
б) Координаты центра: Ц(0;-3) Радиус = 3 ед.
SO -высота пирамиды : SO =10 см ; S(ASC) = S(ABCD) .
Sпол --> ?
Sпол =Sосн+Sбок =a² +4*(a*h/2)=a² +2ah ,где a длина стороны основания , h_апофема:
h =√((a/2)² +SO²) =(1/2)*√(a²+4*SO²) ;
Sпол =a² +a√(a² +4*SO²).
По условию :
S(ABCD)= S(ASC);
a² =a√2* SO/2 ⇒ a =5√2 (см) .
Sпол =a² +a√(a² +4*SO²) =(5√2)² + 5√2 √((5√2)² +4*10²) =50+5√2*15√2 =200 (см²).
ответ : 200 см² .