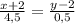, или приведя к целым знаменателям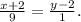 
2√153 см ≈ 24,74 см
Объяснение:
1) 24 - це довжина гіпотенузи; а тому кут, який вона утворює з прямою дорівнює 45°, то обидва катета (один з них - довжина проекції, а інший-висота, відстань від точки до прямої) рівні. Приймемо довжину катета за х.
Тоді, згідно з теоремою Піфагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Довжину другої похилої L знаходимо також за теоремою Піфагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
Відповідь: 2√153 см ≈ 24,74 см
1) 24 - это длина гипотенузы, а т.к. угол, который она образует с прямой равен 45°, то оба катета (один из них - длина проекции, а другой - высота, расстояние от точки до прямой) равны. Примем длину катета за х.
Тогда, согласно теореме Пифагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Длину второй наклонной L находим также по теореме Пифагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
