Объяснение:
АС - основание. Проводим высоты АН2, СН3 и ВН1 соответственно из углов А, С и В.
Высота ВН1, проведённая к основанию является медианой и биссектриссой угла В, тогда СН1 = 12/6 =2
Рассмотрим треугольник ВСН1: cos C = СН1 / ВС = 6/18 =1/3
Расмотрим треугольник АСН2: cos C = CH2 / AC, отсюда СН2 = АС*cos C = 12 * 1/3 = 4
Тогда ВН2 = 18-4 = 14
Согласно теореме: в любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному, т.е. треугольник ВН2Н3 подобен треугольнику АВС. к = ВН2/ВС = 14/18 = 7/9
Н3Н2 = 12*7/9 = 28/3 = 9
ответ;9
Найдем периметр 1ого участка
(60*2+100*2)м=320м
Найдём площадь первого участка:
S1=a*b
S1=6000м
Периметр перыого участка=периметру второго.
Периметр квадрата определяется по формуле:
P=4a
где Р-периметр квадрата, а  - сторона.
- сторона.
По этой формуле находим сторону квадрата
a=80м
Формула нахождения площади квадрата:
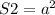
По ней находим площадь квадрата
S2=6400м
Площадь второго участка больше площа первого.
P.S. По одной из теорем: площадь квадрата больше площади прямоугольника, при одинаковых периметрах и при условии P>16
2)Итак, все углы по 60 градусов, значит, треугольник АВС - равносторонний, т.е. АВ=ВС=АС.
3)По условию ВС+АС=4, из пункта 2 следует, что АВ=ВС=АС=2 см. Периметр АВС=2+2+2=6 см.