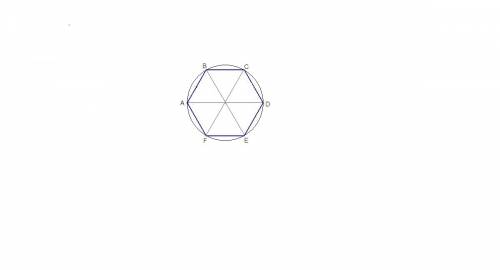
1) В правильном шестиугольнике все стороны равны.
P₆ = 6a₆,
где а₆ - сторона шестиугольника.
6а₆ = 48
а₆ = 8 м
Радиус окружности, описанной около правильного шестиугольника, равен его стороне:
R = a₆ = 6 м
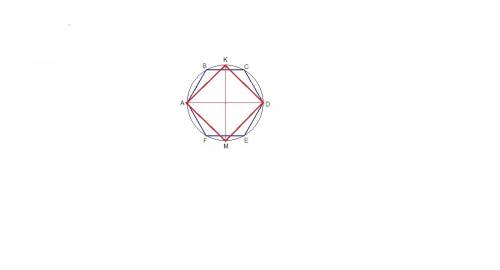
Эта же окружность описана около квадрата.
Радиус окружности, описанной около квадрата:
R = a₄√2 / 2
6 = a₄ √2 / 2
a₄ = 12 / √2 = 6√2 м
2) Шестиугольник диагоналями делится на 6 равных равносторонних треугольников, так как центральный угол его равен 360°/6 = 60°.
Площадь одного треугольника:
S = a²√3/4 = 72√3 / 6
a²√3/4 = 12√3
a² = 48
a = 4√3 см - сторона шестиугольника.
Радиус окружности, описанной около правильного шестиугольника, равен его стороне:
R = a = 4√3 см
Длина окружности:
C = 2πR = 2π · 4√3 = 8π√3 см
В треугольнике две стороны равны 10 см и 17 см, а высота, опущенная на третью, равна 8 см. найти наименьшую из площадей возможных треугольников
Объяснение:
S(треуг)= 1/2*а*h. Пусть АВ=17 см,ВС=10 см, ВН=8 см, ВН ⊥АС.
Возможные треугольники с высотой равной 8 см это ΔАВС, ΔАВН, ΔВСН. У всех перечисленных треугольников одинаковая высота, значит чем меньше основание , тем меньше площадь треугольника.
АС >АН и АС>СН, тк АС это сумма АН и СН.
Т.к ВН-высота, то АВ и ВС наклонные . А чем больше длина наклонной , тем больше проекция : АВ>BC⇒АН>СН.
Значит СН<AH<AC.
ΔCВН-прямоугольный , по т. Пифагора НС=√(10²-8²)=6 (см)
S(ΔCBH)=1/2*6*8=48 (см²)
ЧТОБЫ НАЙТИ ГИПОТЕНУЗУ НАДО:
5²+6²=11²=121