Вчетырёхугольнике авсd диагональ ас образует со сторонами ав и ad равные углы и со сторонами cb cd также равны углы ав=8см вс=10см найдите периметр четырёхугольника abcd в треугольнике авс известно что угола=36* уголв=56*. высоты ау и bf треугольника пересекаются в точке h . найдите углы четырёхугольника 1)cfhe 2)abch желательно скинуть с рисунком

👇

Ответ:

stalkeregor344

18.05.2022

<C=180°-36°-56°=88° (сумма углов треугольника =180°).
<EHF=360°-90°-90°-88°=92° (сумма углов четырехугольника =360°).
1) Углы четырехугольника CFHE равны 88°,90°,92°,90°.
2).<BAE=90°-<B=90°-56°=34 (острые углы прямоугольного треугольника равны 90°).
СР - высота, проведенная к стороне АВ, так как высоты треугольника пересекаются в одной точке. Тогда <BCH=90°-<B=90°-56°=34°.
<AHC=360°-<BAE-<B-<BCH=360°-34°-56°-34°=236°.
Углы четырехугольника АВСН равны 34°,56°,34°,236°.

Вчетырёхугольнике авсd диагональ ас образует со сторонами ав и ad равные углы и со сторонами cb cd т

Вчетырёхугольнике авсd диагональ ас образует со сторонами ав и ad равные углы и со сторонами cb cd т

4,4(32 оценок)

Открыть все ответы

Ответ:

oleksandrskorbat

18.05.2022

Равнобедренного может? Если да , то вот .
В равнобедренном треугольнике биссектрисы, проведённые к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его биссектрисы. Треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, углы LAB и KBA равны как углы при основании равнобедренного треугольника, а углы LBA и KAB равны как половины углов при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB - биссектрисы треугольника ABC - равны. Теорема доказана.
Теорема d3. В равнобедренном треугольнике высоты, опущенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его высоты. Тогда углы ABL и KAB равны, так как углы ALB и AKB прямые, а углы LAB и ABK равны как углы при основании равнобедренного треугольника. Следовательно, треугольники ALB и AKB равны по второму признаку равенства треугольников: у них общая сторона AB, углы KAB и LBA равны по вышесказанному, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Если треугольники равны, их стороны AK и BL тоже равны. Что и требовалось доказать.

4,5(8 оценок)

Ответ:

KatyshaMarina

18.05.2022

В треугольнике ABC ∠С = 90°, AB = 5, tgA = 7/24. Найдите AC.

===========================================================

▪Первый теорема Пифагора ):tgA = BC/AC = 7/24Пусть ВС = 7х, АС = 24х, тогда Применим теорему Пифагора:АС² + ВС² = АВ²( 24х )² + ( 7х )² = 5²576х² + 49х² = 25625х² = 25х² = 1/25 ⇒ х = 1/5 = 0,2 Значит, АС = 24х = 24•0,2 = 4,8▪Второй Тригонометрия ):tg²A + 1 = 1/cos²Acos²A = 1/( tg²A + 1 ) = 1/( (7/24)² + 1 ) = 1/( 625/576 ) = 576/625cosA = ± 24/25 ⇒ ∠A - острый ⇒ cosA = 24/25cosA = AC/AB = 24/25 ⇒ AC = ( 5 • 24 )/25 = 24/5 = 4,8ОТВЕТ: 4,8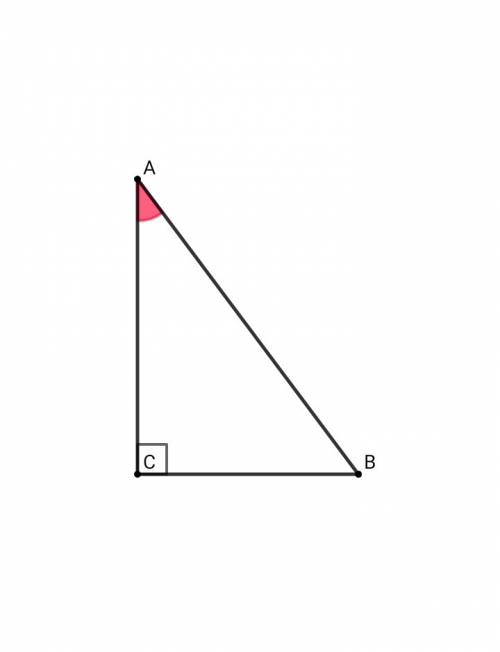
Втреугольнике abc угол c=90 градусов, ab=5, tga=7/24.найдите ac