основание х, боковая сторна 12х. Периметр 12х+12х+х=10 25х=10 х=0,4м.
Проверяем боковая сторона 12*0,4=4,8м, 4,8+4,8+0,4=10
ответ: основание 0,4м
task/21175083 Даны векторы: a = (1; 2) и b = (-2 ; 3)
Найдите значение выражения:
* * * 2a= (2;4) ; -3b =(6 ; -9); (-1/2)a = (-1/2 ; -1) ; (-1/3)b =(2/3 ; -1) ; |a| =√(1²+2²) =√5 ; | b| =√ ( (-2)²+3²) =√13 ; a*b = 1*(-2) + 2*3 = 4 ; a+b =(-1 ; 5 ) ; a - b =(3; -1 ) * * *
4 ) b(a+b) = b*a + b*b = 1*(-2)+2*3 + (-2)*-2) + (3*3) =4 +13 = 17
* * * b*b =|b|*|b|* cos(b^b) =| b |²* 1 =| b |² ( b )² = | b |² * * *
5 ) ( a + b)² = a² +2a*b + b² = |a|² +2a*b + | b |² =(√5)²+2*4+(√13)²=26
* * * ( a + b)² =(-1)² + 5² = 26 * * *
6 ) ( a - b)² = a² - 2a*b + b² = |a|² -2a*b + | b |² =(√5)²-2*4+(√13)²= 10
* * * ( a - b)² =3² + (-1)² = 10 * * *
7 ) ( a + b)(a - b) = a² - b² =(√5)²- (√13)²= 5 - 13 = -8
* * * ( a + b)(a - b) =(-1)*3 ; 5*(-1) = - 8 * * *

Пусть х м - длина основания равнобедренного треугольника, где x>0, тогда длина боковой стороны этого же равнобедренного треугольника по условию равна 12х м, т.к. периметр этого треугольника равен 10 м по условию, получаем уравнение:
х+12х+12х=10
25х=10
х=0,4
Значит, 0,4 м - длина основания.
ответ: 0,4 м.
Теорема Пифагора: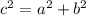 , где с - гипотенуза, а а и b - катеты прямоугольного треугольника.
, где с - гипотенуза, а а и b - катеты прямоугольного треугольника.
К равнобедренному треугольнику она не относится (исключение составляет если основание равнобедренного треугольника является гипотенузой прямоугольного треугольника, т.е. угол, лежащий против основания равнобедренного треугольника - прямой, т.е. равен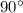 ).
).