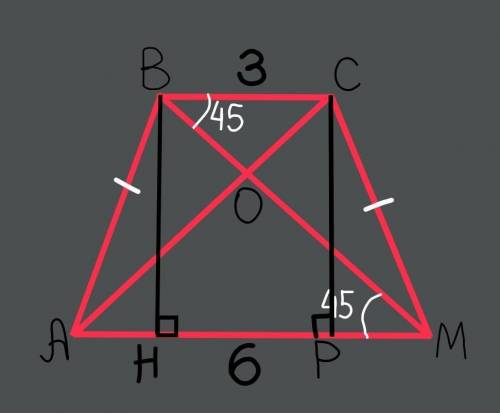
В равнобедренной трапеции диагонали равны и точкой пересечения делятся попарно на равные отрезки. То есть ВО=СО; МО=АО.
Тогда ∆ВОС и ∆АОМ – равнобедренные с основаниями ВС и АМ соответственно.
Следовательно угол ВСО=угол СВО=45° и угол МАО=угол АМО=45°.
Сумма углов в любом треугольнике равна 180°
Тогда угол ВОС=180°–угол ВСО–угол СВО=180°–45°–45°=90°;
Угол АОМ=180°–угол МАО–угол АМО=180°–45°–45°=90°.
Следовательно треугольники ВОС и АОМ – прямоугольные с прямыми углами ВОС и АОМ соответственно.
В прямоугольном треугольнике ВОС по теореме Пифагора:
ВС²=ВО²+СО²
Пусть ВО=СО=х
3²=х²+х²
2х²=9
х²=4,5
х=√4,5
Тоесть СО=√4,5 см
В прямоугольном ∆АОМ по теореме Пифагора:
АМ²=АО²+МО²
Пусть АО=МО=у
6²=у²+у²
2у²=36
у=√18
Тоесть МО=√18 см
Угол СОМ=180°–угол АОМ=180°–90° (так как углы смежные)
Тогда ∆СОМ – прямоугольный с прямым углом СОМ.
Тогда в прямоугольном треугольнике СОМ по теореме Пифагора:
СМ²=СО²+МО²
СМ²=4,5+18
СМ=√22,5
Проведём высоты СР и ВН к стороне АМ.
Высоты трапеции, проведенные из концов одного основания, к другому, паралельны и равны.
Углы образованные высотой и стороной, к которой проведена высота, прямые;
Тогда ВСРН – прямоугольник, следовательно НР=ВС=3.
Получим два прямоугольных треугольника СРМ и ВНА.
СР=ВН так как высоты трапеции равны, АВ=СМ как боковые стороны равнобедренной трапеции
Значит треугольники СРМ и ВНА равны как прямоугольные по гипотенузе и катету.
Следовательно РМ=АН как соответственные катеты.
Тогда РМ+АН=2РМ.
АМ=АН+НР+РМ
АМ=НР+2РМ
6=3+2РМ
РМ=1,5
В прямоугольном треугольнике СРМ по теореме Пифагора:
СМ²=СР²+РМ²
СР²=СМ²–РМ²
СР²=22,5–2,25
СР²=20,25
СР=4,5
ответ: 4,5 см
Радиус описанного круга - это радиус правильного многоугольника, a радиус вписанного круга - его апофема.
1. Стороны правильного многоугольника=8 см. Длина круга вписанного в него=6П см.
Найти длину круга описанного вокруг многоугольника.
Радиус вписанного круга находим из его длины
6п=2пr
r=3 Это апофема этого многоугольника , из чего следует, что радиус его равен 5, т.к. прямоугольный треугольник, катеты которого равны 3 и 4 - египетский и гипотенуза его равна 5. (Хотя можно и теоремой Пифагора воспользоваться).
Радиус описанного круга равен 5, длина его окружности
2пr=2п5=10п
2.Сторона правильного шестиугольника = а. Найти длина его меньшей диагонали.
Длина меньшей диагонали этого шестиугольника - основание равнобедренного треугольника с углом при вершине 120 градусов, или, что одно и то же, диагональ ромба со стороной а. По формуле высоты равностороннего треугольника
d=2а(√3):2=а √3
3.Если правильный 12-ти угольник вписан в круг радиуса R, то его сторона =
R/2:sin 75
Решение:
В правильном 12-ти угольнике каждый центральный угол равен 30°.
углы при стороне равны (180-30):2 =75°
Высота треугольника, образованного радиусами 12 угольника и его стороной, проведенная из угла основания к радиусу, как противолежащая углу 30°, равна половине радиуса R и равна R/2
Из отношения высоты к стороне ( гипотенузе) сторона 12-ти угольника равна R/2:sin 75