Основание ABCD прямоугольного параллелепипеда ABCDA1B1C1D1
является квадратом. Точка M – середина ребра AB, точка К –
середина ребра AD. Через прямую МК проведена плоскость, образующая с плоскостью ABC угол альфа и пересекающая три боковых ребра параллелепипеда. Площадь полученного сечения параллелепипеда равна S. Найдите отрезок AB.
..........................
ответ: АВ=4Ѕсоѕα/5=0,8•Ѕ•соѕα
Объяснение: (Подробно)
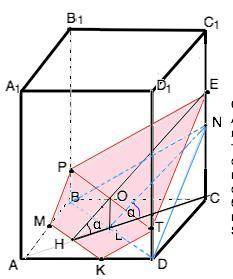
Сделаем рисунок согласно условию. Построение нужного сечения начнём проведением плоскости BDN (на рисунке вложения она ограничена отрезками голубого цвета), образующей угол α с плоскостью основания данного параллелепипеда (NL перпендикулярна BD, CL - её проекция на НС) . (MK//BD; PE//BN; TE//DN, высота HE|| HL– высоте ∆BDN) .
Пересекающиеся МК и ЕН в плоскости МРЕТК соответственно параллельны пересекающимся прямым BD иLN в плоскости BDN=> плоскости параллельны. Данное по условию сечение - плоскость пятиугольника МРЕТК.
Итак, плоскость МРЕТК образует с плоскостью АВС угол α и пересекает три боковых ребра параллелепипеда.
Диагонали основания – AC=BD=АВ:sin45°=АВ√2 Для удобства АВ в записи решения опускается до окончательного ответа.
В МРЕТК проведем РТ||BD=√2
MK=BD/2=(1/2)•√2 (средняя линия ∆ АBD)
AH=1/2 AL=(1/4)•√2
CH=(3/4)√2)
Параллелепипед прямоугольный. =>
Из⊿ EHС гипотенуза ЕН=CH/cosα=(3√2)/4cosα.
ЕН и РТ пересекаются в т.О. Перпендикуляр OL отсекает от треугольника ЕНС подобный ему ∆HOL => k=HL:НC=НО:НЕ=1/3=>
НО=НЕ/3=( √2)/4cosα.
ОЕ=2НО=(√2)/2•соѕα
Ѕ(MPETD)=S(PET)+S(МРТК)
S(PET)=РТ•ЕО/2=0,5•√2•(√2)/2соѕα =1/2соѕα
Ѕ(МРТК)=ОН•(МК+РТ)/2=3/4соѕα
Ѕ=3/4соѕα+1/2соѕα =5/4соѕα
Подставим пропущенное АВ.
Ѕ=АВ•5/4соѕα=>
АВ=4Ѕсоѕα/5=0,8•Ѕ•соѕα
Объяснение:
1. Точка Т – середина отрезка МР. Найдите координаты точки Р,
если Т (-2;4) и М (-6; -7).
2. a)АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (9; -2) и В (-1;-6).
b)Запишите уравнение окружности, используя условия пункта а).
3. Дано: A(2;4)Bина отрезка МР. Найдите координаты точки Р,
если Т (-2;4) и М (-6; -7).
2. a)АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (9; -2) и В (-1;-6).
b)Запишите уравнение окружности, используя условия пункта а).
3Найдите координаты точки Р,
если Т (-2;4) и М (-6; -7).
2. a)АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (9; -2) и В (-1;-6).
b)Запишите уравнение окружности, используя условия пункта а).
3. Дано: A(2;4)B(-2;3)C(-1;5) Напишите уравнение медианы ВМ.
Т (-2;4) и М (-6; -7).
2. a)АВ – диаметр окружности с центром О. Найдите координаты центра одите координаты точки Р,
если Т (-2;4) и М (-6; -7).
2. a)АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (9; -2) и В (-1;-6).
b)Запишите уравнение окружности, используя условия пункта а).
3. Дано: A(2;4)B(-2;3)C(-1;5) Напишите уравнение медианы ВМ.
4.Точки А(-3;-4), В(5;-4), С(5;8), D(-3;-1) – вершины прямоугкружности, если А (9; -2) и В (-1;-6).
b)Запишите уравнение окружности, используя условия пункта а).
3. Дано: A(2;4)B(-2;3)C(-1;5) Напишите уравнение медианы ВМ.
4.Точки А(-3;-4), В(5;-4
4.Точки А(-3;-4), В(5;-4), С(5;8), D(-3;-1) – вершины прямоугольной трапеции с основаниями ВC . Дано: A(2;4)B(-2;3)C(-1;5) Напишите уравнение медианы ВМ.
4.Точки А(-3;-4), В(5;-4), С(5;8), D(-3;-1) – вершины прямоугольной трапеции с основаниями ВC и АD, А(-2;3)C(-1;5) Напишите уравнение медианы В