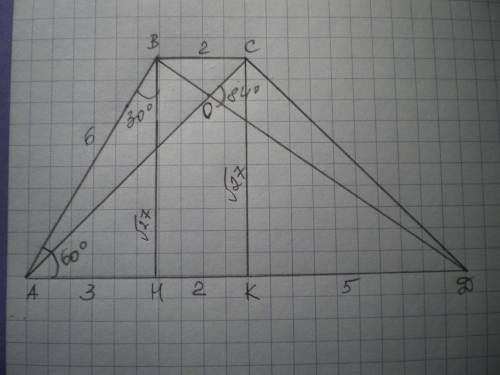
Проведем высоту ВН. ΔАВН - прямоугольный, ∠А=60°, тогда ∠АВН=30°, а АН=1\2 АВ=3.
Из ΔАВН найдем ВН
ВН=√(АВ²-АН²)=√(36-9)=√27.
Если основание АД=10, то ВС=10:5=2.
Проведем высоту СК=ВН=√27.
НК=ВС=2. АК=АН+КН=3+2=5; КД=АД=АК=10-5=5.
Найдем АС из ΔАСК. АС²=АК²+СК²=25+27=52. АС=√52=2√13.
Найдем ВД из ΔВДН, где ДН=КН+КД=2+5=7. ВД²=ВН²+ДН²=27+49=76. ВД=√76=2√19.
Найдем ∠СОД по формуле площади трапеции
S=1\2 d₁*d₂*sinα
найдем площадь по формуле S=1\2 (АД+ВС)*ВН=1\2 * (10+2) * √27 = 18√3.
18√3=1\2 * 2√13 * 2√19 * sin∠СОД
18√3=2√247 * sin∠СОД
sin∠СОД=15,6\15,7=0,9936
∠СОД=84°
ответ: 2√13 ед.; 2√19 ед; 84°
В прямоугольном параллелограмме квадрат ее диагонали равен сумме квадратов длин ее сторон.
А1С2 = АА12 + АД2 + СД2.
АА12 = А1С2 – АД2+ СД2 = 676 – 64 – 36 = 576.
АА1 = 24 см.
ответ: Боковое ребро равно 24 см.
второй
ABCDA1B1C1D1 - параллелепипед
1) основание ABCD:
в треугольнике АВС
L B = 90 град.
AB = 6 см
BC = 8 см =>
AC^2 = AB^2 + BC^2 = 6^2 + 8^2 = 100 = 10^2 =>
AC = 10 см - диагональ основания
2) В треугольнике ACC1:
L ACC1 = 90 град.
AC = 10 см
AC1 = 26 см =>
CC1 = AC1^2 - AC^2 =
= 26^2 - 10^2 =
= (26+10)(26-10) =
= 36*16 = 6^2 * 4^2 =
= (6*4)^2 = 24^2 =>
CC1 = 24 см - высота параллелепипеда
решение представлено на фото
Объяснение: