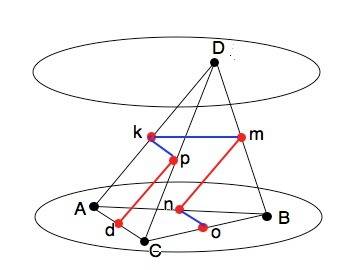
Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
в прямоугольном треугольники сторона на против угла в 30 градусов равна половине гипотенузы, следовательно АВ=8
Р=2(8+10)=9
угол А (в треугольнике АВК) = 180-90-30=60
угол D=180-60=120
угол С=180-120=60
угол В=180-60=120