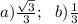
Объяснение:
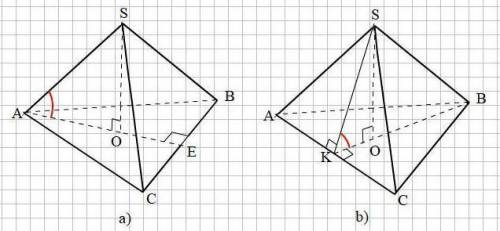
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
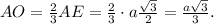
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
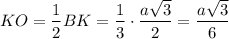
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.

8. На первом рисунке прямоугольный треугольник, сумма углов при катетах равна 90, значит, угол А равен 90-23=67. На втором равнобедренный, углы при основе равные, значит угол С=57. Находим А, так как сумма углов треугольника равна 180, то угол А= 180-(уголВ+уголС)=180-(57+57)=56 градусов. На третьем рисунке сумма углов треуголника равна 180, значит угол А=180-(100+55)=25 градусов. в итоге, больше всего градусов имеет угол А на первом рисунке))
9. угол равностороннего равен 60. 60:4=15.
Надеюсь мой ответ не удалят опять))