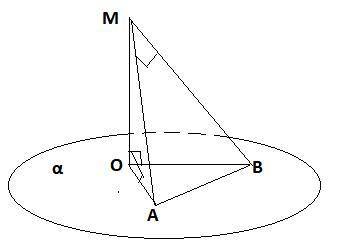
Из точки находящийся на расстоянии корень с 3 см от плоскости проведен к этой плоскости две наклонные которые наклонены к плоскости под углами 45° и 60°. Найдите расстояние между основаниями наклонных если наклонные перпендикулярны.
Объяснение:
Т.к ОМ -расстояние и ОМ⊥α, то ОМ⊥ОВ и ОМ⊥ОА .
ΔОМА-прямоугольный ,∠ОАМ=45° ⇒ ∠ОМА=45° поэтому
ОМ=ОА=√3 см . Найдем по т. Пифагора МА=√(√3²+√3²)=√6 (см).
ΔОМВ -прямоугольный, ∠ОВМ=60° , sin 60=OM/MB ,√3/2=√3/МВ , МВ=2 см.
ΔОМВ -прямоугольный,по т. Пифагора АВ=√(МА²+МВ²)=√(6+4)=√10 (см)
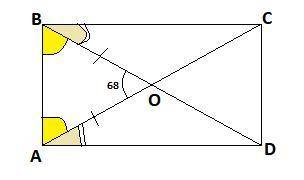
" В прямоугольнике ABCD, где AC и BD диагонали пересикающиеся в точке О, угол AOB=68 градусов. Найти углы ABO, CBO, BAO и вас, через дано найти решение с чертежом"
Объяснение:
Дано :АВСD-прямоугольник,О-точка пересечения диагоналей , ∠АОВ=68°.
Найти :∠АВО, ∠СВО,∠ВАО, ∠DАО.
Решение.В прямоугольнике диагонали равны и точкой пересечения делятся пополам ⇒ОА=ОВ=ОС=ОD.
Значит ΔАВО-равнобедренный и углы при основании равны : ∠АВО=∠ВАО=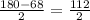 
=56° .
∠СВО=90°-56°=34° , т.к все углы прямоугольника по 90°.
∠DАО=90°-56°=34°
Площадь квадрата равна квадрату его стороны