Объяснение:
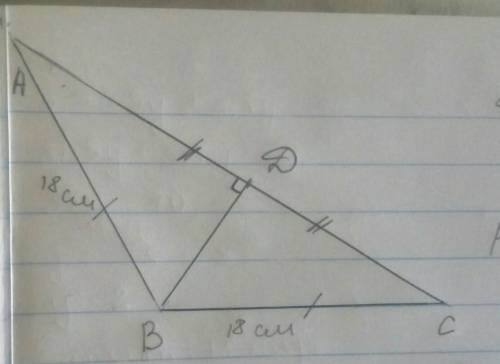
1) Т.к. АВ=ВС, то треугольник АВС-р/б, следовательно, ВD - медиана, биссектриса, высота.
Т.к. ВD - биссектриса, то в треугольнике АВD угол АВD= 120°:2=60°
Т.к. ВD - высота, то в треугольнике АВD угол АDВ = 90°
Сумма углов треугольника равна 180°, следовательно, угол ВАD = 180°-(60°+90°)=180°-150°=30°.
2) Мы узнали, что угол ВАD=30°, найдём длину ВD.
Треугольник АВD - прямоугольный.
В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.
Угол ВАD = 30°, угол ВАD лежит напротив ВD, следовательно ВD = 0,5АВ=0,5×18=9 (см).
ответ: 1) 60°, 90°, 30°.
2) 9 см.
Вот чертёж, дано, надеюсь, напишешь.
(-2,2; -0,6)
Объяснение:
Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
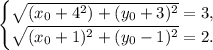
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно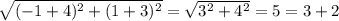 
. Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо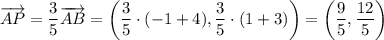 
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор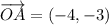 
, мы получим координаты точки P(x₀, y₀): 
.
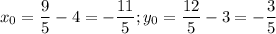Решением системы является точка (-2,2; -0,6).
Решаем ро формуле d1^2+d2^2=4a^2
3600+6400=4a^2
10000=4a^2 /4
a^2=2500
a=50cм(тоесть сторона ромба равна 50 см)
Периметр=50*4=200см