угол С равен 30 градусов, т.к. в треугольнике один 90, а другой 60. По свойству: против угла в 30 градусов лежит катет, равный половине гипотенузы. Сторона СА равна 15 см. Далее по теореме Пифагора ВС в квадрате равна АС в квадрате плюс ВА в квадрате. Находим ВА. как корень квадратный из 30 в квадрате минус 15 в квадрате. А площадь прямоугольного треугольника равна половине произведения катетов
Если один из углов ромба равен 60°, второй равен 120° ( из суммы внутренних углов между параллельными прямыми и секущей). Поэтому его меньшая диагональ делит его на два равносторонних треугольника и равна стороне ромба.
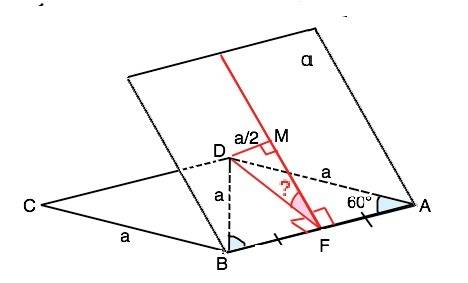
а) CВ║АВ, лежащей в плоскости α и, следовательно, параллельна этой плоскости (свойство). Расстояние от точки до плоскости равно длине перпендикуляра между ними. Все точки прямой, параллельной какой-либо плоскости, равноудалены от неё. ⇒ Расстояние от точки С до плоскости α равно расстоянию от точки D до неё, т.е. а/2.
б). Линейный угол двугранного угла определяется лучами, проведенными в гранях угла из одной точки ребра перпендикулярно ему.. На рисунке DF – высота ∆ АDВ. DF⊥АВ, DM перпендикулярна α, МF – проекция DF на плоскость α. По т.о 3-х перпендикулярах МF⊥АВ. Угол МFD – искомый.
в) DF⊥АВ, DF=a•sinDAF=a√3/2. Из ∆ DMF sinDFM=a/2:a√3/2.=1/√3
дано
тр. ABC
угол A=90
угол B=60
BC (гипотенуза) = 30 см
найти
S-?
решение
S=1/2*a*b
угол C=180-90-60=30
Значит из сво-ва - катет лежащий против угла в 30 равен пловины гипотенузы ⇒
AB=1/2BC=1/2*30=15 см
по т. Пифагора:
AC=√BC²-AB² = √30²-15²=√900-225=√675=15√3 см
S=1/2*15*15√3=112.5√3 см ²
ответ
площадь треугольника равна 112,5√3 см²