ответ: 12 (ед. длины)
Объяснение:
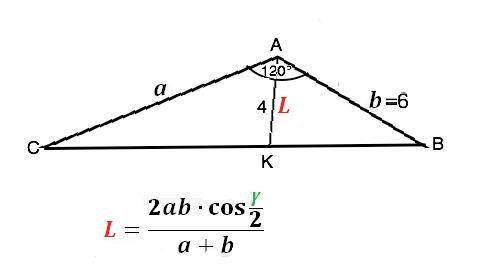
Одна из формул биссектрисы треугольника
L={2ab•cos(0,5γ)}:(a+b) ,
где L биссектриса, а и b- стороны, γ - угол между ними.
На приведенном рисунке АК - биссектриса ∆ АВС, АС=а, АВ=6, угол А=γ =120°
cos0,5γ=cos60°=1/2
4=2a•6•0,5/(a+6) =>
4a+24=6a =>
АС=a=12 (ед. длины)
Или с тем же результатом найти:
1) По т. косинусов из ∆ АКВ найти КВ
2) по т. синусов из ∆ АКВ угол В
3) из суммы углов треугольника угол С
4) по т. синусов вычислить длину искомой стороны АС
если x не равно 0, то разделив левую и правую части уравнения на x, получим
m =((5-y)/x) n, где ((5-y)/x) какое-то число.
По условию коллинеарности:Два вектора a и b коллинеарны, если существует число не равное нулю n такое, что a = n · b
Следовательно, если a и b не коллинеарны то такого числа не существует.
А в нашем примере такое число есть (при x не равном 0).
Следовательно если x не равно 0, то векторы коллинеарны.
А так как по условию они не коллинеарны, то x = 0. Тогда и y = 0.
ответ: x = 0 и y = 0