y = kx + 5
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)k = - 4
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)k = - 4Уравнение функции : у = -4х + 5
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)k = - 4Уравнение функции : у = -4х + 5ответ : при k = -4 график функции проходит через точку D(6; -19) .
DB= 1 ед.
Объяснение:
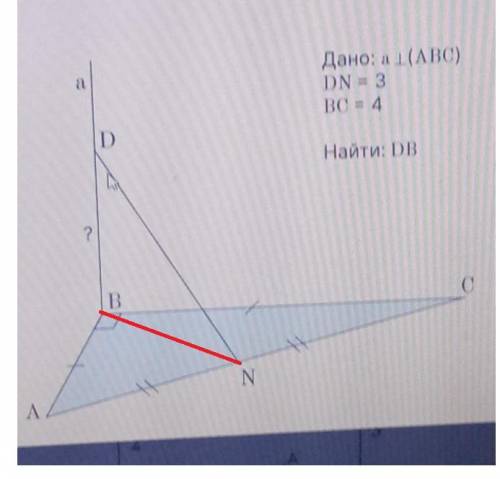
Рассмотрим рисунок. Треугольник Δ АВС - прямоугольный, так как ∠В=90° и равнобедренный, так как АВ=ВС. По условию АВ=ВС=4 ед.
Найдем гипотенузу АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
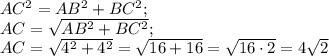
По рисунку понятно, что N- середина АС и тогда отрезок BN - медиана прямоугольного треугольника АВС.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
Значит,
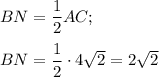
Так как по условию а ⊥ (АВС), то она перпендикулярна любой прямой, лежащей в этой плоскости.
Тогда а⊥ BN и ΔDBN - прямоугольный.
Применим теорему Пифагора и найдем DB.
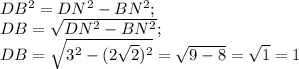
DB= 1 ед.
Сумма двух смежных углов равна 180 гр.
х+5х=180
6х=180
х=30 - величина одного угла, 180-30=150 - величина второго угла
2.
Сумма 4 углов, который образуются при пересечении прямых = 360 градусов
Вертикальные углы, которые образуются попарно равны.
Поэтому два угла будут равны по 48 гр. каждый, а два других = 360-(48*2)=264 в сумме, то есть 264/2 каждый = 132 гр.
Уравнением можно записать так:
2*48 + 2*х=360
96+2х=360
2х=264
х=132
3.
Вертикальные углы равны, а их сумма = 48 гр.
Значит:
2х=48
х=24 гр.