Стороны правильного многоугольника равны.
Диаметр окружности, вписанной в квадрат со стороной m, равен длине его стороны.
d=m, r=d:2=m/2
Периметр квадрата=16 дм, => m=16:4=4 (дм) => r=4:2=2 (дм)
Длину стороны а правильного n-угольника, вписанного в окружность, находят по формуле
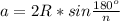
R=r=2 дм
n=5
180°:5=36°
sin36°= ≈0,5878
P=5a=10•2•0,5878= ≈11,7557 дм
Вариант решения:
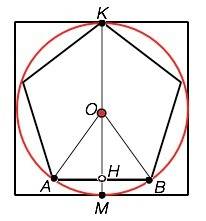
Рассмотрим рисунок приложения.
АВ- сторона пятиугольника., О - центр описанной окружности.
ОН - высота, медиана и биссектриса равнобедренного ∆ АОВ
Центральный угол АОВ вписанного пятиугольника 360°:5=72°
Угол АOН= 72°:2=36°
АН=ОА•sinАОН=2•sin36°, AB=2AH=4•sin36°
AB=4•0,5878 =≈2,35 (дм)
Периметр правильного пятиугольника со стороной а равен 5а
Р=5•АВ=≈11,7557 (дм)