Площадь круга, как Вы помните, находят по формуле
S=πr²
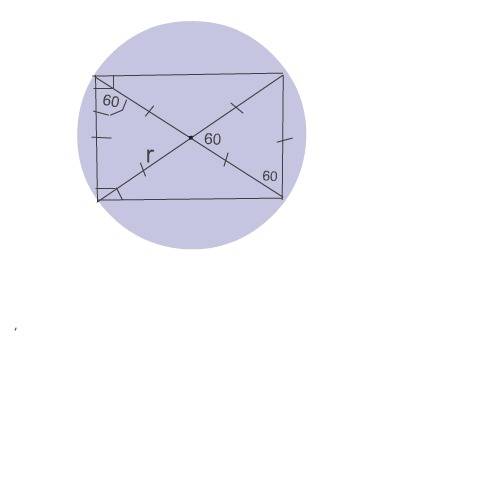
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
AB=16
∠B=30°
По теореме синусов, стороны пропорциональны синусам противолежащего угла.
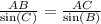
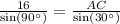
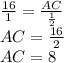
(Ну короче на будущее, катет прямоугольного треугольника лежащий напротив угла 30° равен половине гипотенузы)
Радиус вписанной окружности в прямоугольный треугольник вычисляется по формуле:
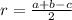
a и b – катеты, c – гипотенуза
a=8
c=16
Найдем b по теореме Пифагора
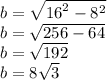
(Еще раз на будущее катет прямоугольного треугольника, лежащий напротив угла 60°, в √3 раза больше, чем катет который напротив 30°)
Теперь найдём радиус:
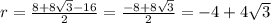
Длина окружности:
L=2πr
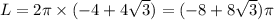
Можно дальше скобки раскрыть, если понадобится.
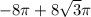
Но я думаю это необязательно
1)стороны 15см, 20 см, 30 см, относятся как 3:4:6
2) всего частей получается (3+4+6=13) 13
3) 26:13=2 тоесть в одной части 2 см
4) 3*2=6см (сторона треугольника которая подобна стороне в 15 см)
5)4*2=8см (сторона треугольника которая подобна стороне в 20 см)
6)6*2=12см (сторона треугольника которая подобна стороне в 30 см)
ответ: 6см, 8см, 12см