ответ: 21 (ед. длины)
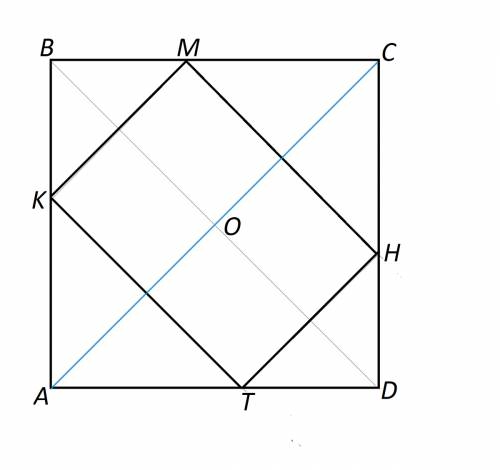
Объяснение: Поскольку стороны вписанного прямоугольника параллельны диагоналям квадрата, диагональ ВD квадрата делит периметр прямоугольника на две равные половины ТКМЕ и ТРНЕ. Как известно, диагонали квадрата делят его углы пополам. При этом угловые треугольники МВН и КDР – равные прямоугольные равнобедренные, в которых ВЕ=ЕМ=ЕН и TD=ТК=РТ. Заметим, что МК+МЕ+ТК=DВ=10,5 - это длина половины периметра прямоугольника. Полный периметр прямоугольника КМНР=2•10,5=21 ( ед. длины)
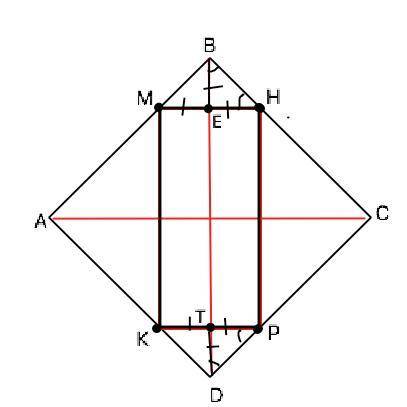
Дан равносторонний ΔABC. Медиана BM=12√3.
Найти сторону ΔABC.
В правильном треугольника медиана является и высотой, откуда BM⊥AC.
Углы между сторонами правильного треугольника равны по 60°, поэтому ∠BCA=60°.
В прямоугольном ΔВМС (∠М=90°): BM=12√3, ∠BCM=60°;
синус острого угла в прямоугольном треугольнике это отношение противолежащего катета к гипотенузе, откуда
sin∠BCM = BM/BC ⇒ BC=BM/(sin∠BCM)
BC=(12√3)/(sin60°)=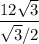 = 12·2=24
= 12·2=24
ответ: 24.