Пусть высота трапеции х
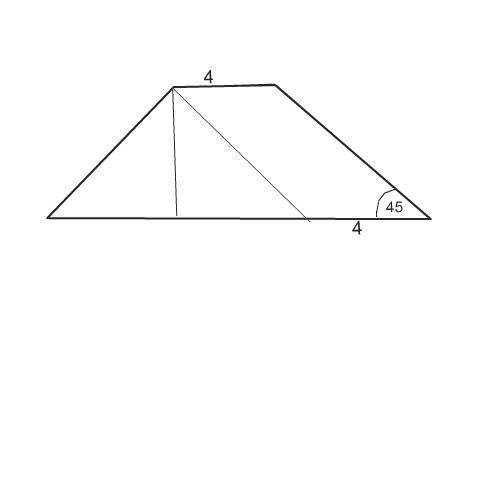
Проведем параллельно боковой стороне прямую. Она отсечет от трапеции прямоугольный равнобедренный треугольник с углами при основании 45 градусов, половина основания которого равна высоте и меньшему основанию.
Тогда большее основание 2х+4
Полусумма оснований
(2х+4+4):2=(2х+8):2=х+4
Площадь трапеции
х(х+4)=117
х²+4х-117=0 Решим это уравнение:
D = b² - 4ac = 484
√D = 22
х1=9
х2= -13 (не подходит)
Боковую сторону по свойству диагонали квадрата и гипотенузы равнобедренного прямоугольного треугольника найдем по формуле
а√2
Она равна 9√2 см
1.опустим высоту вк
2.раз окружность делит стороны трапеции на 2 и 8, то см 2 и мd=8
аналогично bh=2 и ha=8 так как трап равнообокая
3. раз окр вписана в трапецию то ah=ap=pd=dm=8 и bh=bt=t=cm=2 так как трапеция равнобокая и ah,ap,dp,dm,mc,ct,tb,bh являются касательными проведенными из одной точки а значит они равны
4.итак треугольник abk прямоугольный(bk-высота) то по теореме пифагора
ab^2=ak^2+bk^2
100=4+bk^2 где ak=(ad-bc)/2
bk=корень из 96
5. итак площадь равна=0.5*корень96*20=40корней из 6
Сделаем по условию задачи рисунок окружности между прямыми.
Из точки М опустим перпендикуляр к одной из прямых. Обозначим точку проекции М1.
Пересечение этого отрезка с окружностью обозначим К.
Из центра О опустим перпендикуляр на ту же прямую. Обозначим О1.
Соединим радиусами точки М и К.
Проведем отрезок, перпендикулярный хорде МК.
Расстояние КМ1 равно расстоянию от М до другой прямой = 3 см.
МК=15-(3+3)=9
Радиус окружности равен половине расстояния между параллельными и равен 15:2=7,5
Расстояние между проекциями точки М и центра окружности О1М1= ОН
ОН по теореме Пифагора равно
ОН=√(ОМ²-МН²)=√36=6
Расстояние между проекциями точки М и центра окружности равно 6 см