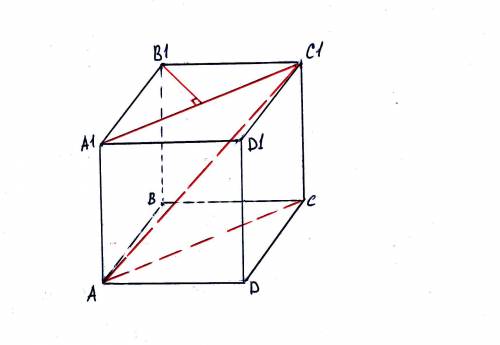
Так легко же все. Смотрите, АС1 лежит в плоскости АА1С1С (сечение через диагонали верхней и нижней граней и боковые ребра). ВВ1 параллельна этой плоскости. Поэтому расстояние между скрещивающимися прямыми АС1 и ВВ1 равно расстоянию между ВВ1 и плоскостью АА1С1С. Уточняю - где то на ВВ1 есть точка, которая проектируется на плоскость АА1С1С, и проекция попадает на АС1, если быть совсем точным, эта точка находится в центре куба, но это не важно - от любой точки ВВ1 до плоскости АА1С1С расстояние одно и то же. Осталось найти это расстояние. Но оно равно расстоянию от вершины В до диагонали АС квадрата АВСD, то есть
ответ а*корень(2)/2.
Раз трапеция равнобедренная, то и диагонали равны (ну рассмотрите пару треугольников, образованных РАЗНЫМИ ДИАГОНАЛЯМИ, большим основанием и боковой стороной, из их равенства по 2 сторонам и углу между ними следует и равенство третьих сторон, то етсь диагоналей).
Типовое построение - проводим через вершины малого основания прямую II диагонали, НЕ проходящей через эту вершину, до пересечения с продолжением большого основания. Получается треугольник, РАВНОВЕЛИКИЙ (имеющий ту же площадь) трапеции (у него основание равно сумме оснований трапеции, а высота - общая с трапецией).
Этот треугольник В ДАННОМ СЛУЧАЕ равнобедренный прямоугольный с гипотенузой 64. Поэтому его площадь равна 32*64/2 = 1024
(32 - это высота, она же медиана к гипотенузе, равна половине гипотенузы)
<ADB=<ADC по условию
AD-общая
Треугольники ADB и ADC равны по стороне и 2 прилежащим углам
Значит АВ=АС