Длина стороны ав треугольника авс составляет 40% от его периметра, а длина стороны вс - 70% от длины стороны ав. длина стороны ав на 2 см больше, чем длина стороны ас. сколько процентов составляет длина стороны ас от периметра треугольника авс? , найдите периметр треугольника авс?
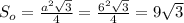 - площадь основания
- площадь основания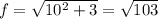 см
см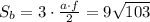
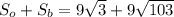
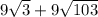

АВ=(x+2)
BC=0,7AB=0,7(x+2)
P=AB+BC+AC=(x+2)+0,7(x+2)+x=2,7x+3,4
По условию длина стороны АВ =(х+2) составляет 40% от периметра (2,7х+3,4)
Составим уравнение
х+2=0,4·(2,7х +3,4)
х+2=1,08х+1,36
0,08х=0,64
х=8
Р=2,7x+2=2,7·8 + 3,4=25 см
25 составляют 100%
8 составляют х %
х=8·100:25=32%
ответ. АС составляет 32% от периметра
Р=25 см