Объяснение (подробно):(см. рисунок приложения.)
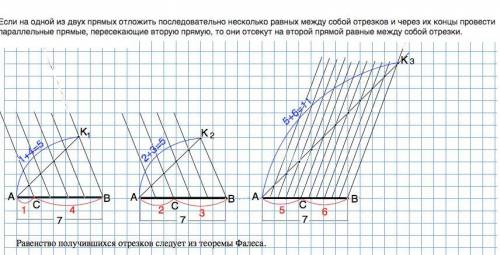
Чертим отрезок АВ=7 см. Из А проведем луч и отложим на нем равные отрезки заданным числом. Конец последнего отрезка соединим с концом В заданного отрезка. Через концы отложенных на луче отрезков проведем прямые, параллельные прямой ВК. (Если не помните, как провести прямую, параллельную данной, найдите в учебнике, и в интернете на эту тему много информации).
а) на проведенном луче отложим 1+4=5 равных отрезков. Прямые, параллельные К1В, делят АВ на 5 равных частей. Часть АС=1, часть СВ=4. Длину получившихся отрезков можно посчитать на калькуляторе.
АС=7:5•1 (см); СВ=7:5•4(см)
б) отрезок АВ тем же делим на 2+3=5 частей.
АС=7:5•2 (см); СВ=7:5•3 (с м)
в) аналогично на проведенном луче отложим 5+6=11 равных частей, и отрезок АВ делится на 11 равных частей.
АС=7:11•5 (см); СВ=7:11•6 (см)
Берем линейку и карандаш, строим рисунок.
Очевидно, становится из рисунка, что, если внешний угол равен 135 градусам.
Тогда, поскольку внешний угол равен сумме двух других углов треугольника, то
первый непрямой угол будет равен 135-90= 45 градусов. Второй угол, соответственно, 180-90-45= так же 45 градусов.
Второе решение: внешний угол с прилежащим к нему углом треугольника составляют 180 градусов. Тогда, угол треугольника, прилежащий к внешнему, равен 180-135= 45 градусов. Третий угол так же равен 180-45-90 (треугольник прямоугольный) = 45 градусам.
ответ: острые углы этого треугольника равны между собой и равны 45 градусам.
Смотри, площадь боковой поверхности треугольной пирамиды - это три треугольника. При условии что пирамида правильная, значит треугольники равнобедренные. Сначала найдем площадь одного треугольника(боковую площадь дели на три). SP - медиана, а соответственно биссектриса и высота треугольника SAB(т.к. он равнобедренный). Площадь треугольника равна половине основания умноженного на высоту. Выражаешь из этого основание, все остальное тебе дано(Короче находишь AB). В основании правильной пирамиды лежит правильный треугольник(равносторонний). Значит AB=BC=AC=тому что ты там насчитаешь. Вроде как то так...