Объяснение:
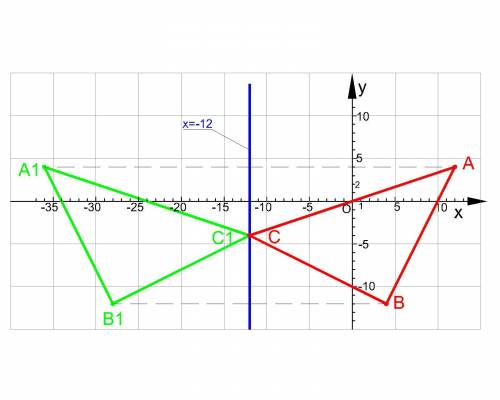
1. Выполняем построение треугольника АВС.
2. Строим график прямой х = -12 . Это вертикальная прямая проходящая через точку (-12; 0)
3. Выполняем построение симметричной фигуры:
от т. А проводим перпендикуляр к прямой х = -12. Откладываем перпендикуляр такой же длины в противоположною сторону от х = -12.
То же самое выполняем для т. В. Т. С совпадает с точкой С1, т.к. абсцисса т. С = -12 и лежит на прямой х = -12.
Координаты ΔA1B1C1 можно определить графически:
А1(-36;4) , В1(-28; -12) , С1(-12; -4).
Также абсциссы можем определить математически:
х1 = -12 - (12+х) = -24-х.
Здесь -12 - это сдвиг координат влево на 12 единиц, (12+х) расстояние между осью симметрии и точками исходного треугольника.
Ординаты остаются неизменными, т.к. ось симметрии - вертикальная.
АВСА1В1С1 – прямая треугольная призма, АС = ВС = 10, АВ = 12,
О – точка пересечения медиан, угол C1ОC = 45˚. Найти объем призмы.
-----------
Объем V призмы находят произведением площади её основания на высоту.
V=S•H
В ∆ ОСС1 - угол С1ОС=45º, угол С1СО=90º (т.к. призма прямая и все её ребра перпендикулярны основанию)⇒ второй острый угол ∆ ОСС1 равен 45°. ⇒ ∆ АВС - равнобедренный и СС1=Н=ОС.
Точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины. ⇒
ОС=2/3 медианы СН.
СН в равнобедренном треугольнике - высота, ∆ АНС- прямоугольный.
СН=8 ( отношение катета АН к гипотенузе АС в ∆ АНС= 3:5, следовательно, ∆ АНС - египетский. Можно СН и по т.Пифагора найти)
СС1=ОС=8•2/3=16/3
S (∆ ABC)=CH•AH=8•6=48
V=48•16/3=16•16=256 (ед. площади)
