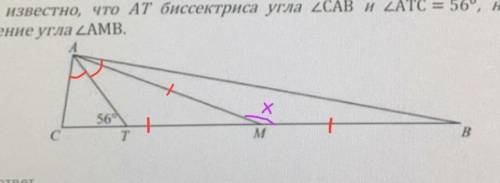
Так как точка М – середина ВС, то АМ – медиана ∆АВС, а СМ=МВ,
АМ=СМ по условию, получим что СМ=МВ=АМ.
Треугольник является прямоугольным, если его медиана делит противоположную сторону на отрезки, равные себе.
Следовательно ∆АВС – прямоугольный с прямым углом САВ.
АТ – биссектриса угла САВ по условию, следовательно угол САТ=угол САВ÷2=90°÷2=45°.
В треугольнике сумма всех углов равна 180°.
Тогда: угол АСТ=180°–угол САТ–угол АТС=180°–45°–56°=79°;
Угол АВС=180°–угол САВ–угол АСВ=180°–90°–79°=11°.
Так как АМ=МВ, то ∆АМВ – равнобедренный с основанием АВ.
Углы при основании равнобедренного треугольника равны.
Значит угол МАВ=угол МВА=11°.
Так как сумма всех углов в треугольнике равна 180°, то угол АМВ=180°–угол МАВ–угол МВА=180°–11°–11°=158°.
ответ: 158°
118°, 118°, 62°, 62°
Объяснение:
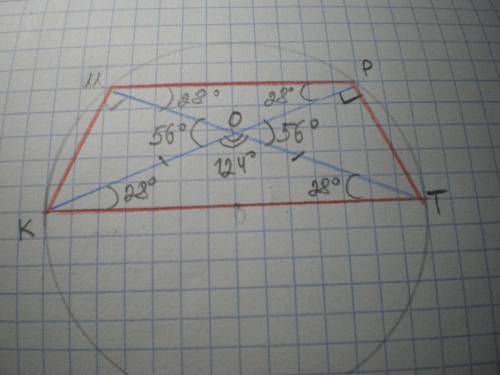
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
следовательно ответ под номером B