 (выделена оранжевым)
(выделена оранжевым) .
.  и
и  :
:


 .
. через
через  найдем
найдем 

 , найдем котангенс этого угла:
, найдем котангенс этого угла:
 ,
,



Площадь выпуклого многоугольника можно посчитать по известной формуле:
S = p•r , где р - это полупериметр , r - радиус вписанной окружности.
Если в четырёхугольник вписана окружность, то сумма её двух противолежащих сторон равна сумме двух других противолежащих сторон.
Боковые стороны в равнобедренной трапеции равны, поэтому сумма противоположных сторон равна: 70 + 70 = 140 см, и ещё + 140 см, получаем периметр трапеции = 280 см, но нам нужен полупериметр, поэтому 280/2 = 140 см
S = p•r = 140•25 = 35•4•25 = 3 500 см^2
ответ: 3 500 см^2
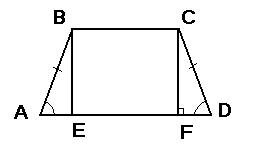
Площадь трапеции = (а+в)*h/2, где а и в - основания трапеции, h-высота. Если опустить из вершины верхнего основания высоту, то получится прямоугольный треугольник АВЕ(на рисунке). Если внимательно его рассмотреть, то мы увидим, что есть прямой угол(90 градусов) и угол при основании равен 45 градусов(угол А), значит угол АВЕ равен 45 градусов(т.к. в треугольнике все три угла в сумме составляют 180 градусов). Отсюда следует, что АЕ=ВЕ, и будут они равны в корень из двух меньше гипотенузы, т.е. 5(т.к. гипотенуза равна 5 корней из двух). ВС=10(меньшее основание) и оно будет равно ЕF. А АЕ=FD(трапеция равнобокая)=5. Значит найдем большее основание = AE+EF+FD=5+10+5=20. ЕВ=h=5. Подставляем в формулу площади S=(10+20)*5/2=150/2=75.
ответ: 75
Значит их тангенсы равны, т.е. HD/DC=BD/AD, откуда BD*DC=AD*HD.
Но т.к. точка M лежит на окружности, то MD - высота прямоугольного треугольника BCM, значит BD*DC=MD². Значит AD*HD=MD², т.е. HD=MD²/AD=15²/45=5. Отсюда AH=AD-HD=45-5=40.