16 см
Объяснение:
1) По св-ву ромба:
АО = ОС = 15 смOD = OB AС _|_ BD => ∆ AOB - п/у2) Расм. ∆АОВ - п/у :

=> ВD =16см (по док выше)

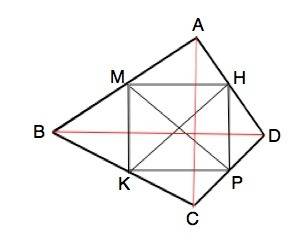
Смотрим рисунок, данный в приложении.
Диагонали выпуклого четырехугольника делят его на треугольники. Стороны четырехугольника, которые соединяют середины сторон ABCD, являются средними линиями таких треугольников, поэтому противоположные стороны такого вписанного четырехугольника равны и параллельны.⇒
Четырехугольник КМНР - параллелограмм.
Отрезки, соединяющие середины сторон исходного четырехугольника - диагонали получившегося параллелограмма.
Если диагонали параллелограмма равны, этот параллелограмм– прямоугольник. Противоположные стороны КМНР равны половине диагоналей АВСD.
Примем длину ВD= а. Тогда АС=3а/4
КР=ВD:2=а/2
КМ=АС:2=3а/8
По условию диагонали прямоугольника равны 15.
Вычислим по т.Пифагора стороны КМНР.
МР²=КМ²+КР²
15²=(3а/8)²+(а/2)²
225=9а²/64+а²/4 ⇒
25а²/64=225 откуда
а²=576
а=24
КР=МН=24:2=12
КМ=РН=24:8•3=9
Сумма квадратов диагоналей равна сумме квадратов всех сторон. d(1)^2+d(2)^2=4a^2, где d(1)=30см, а =17см, подставим данные в формулу:
d(2)^2+30^2=4*17^2
d(2)^2=1156-900=256,
d(2)=16 (cм).
ответ : 16 см вторая диагональ.