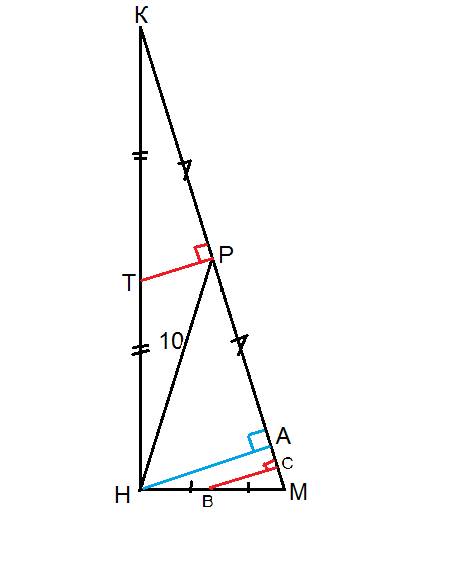
Пирамида, в основании равносторонний треугольник АВС, ВН-высота треугольника, точка О центр - пересечение высот(медиан биссектрис), ОК-высота пирамиды, КН-апофема, АН-ребро=6, tg углаКНО=2*корень11, ОК=ОН*tgКНО=ОН*2*корень11, проводим высоту АМ, треугольник АКО - ОК=корень(АК в квадрате-АО в квадрате)=корень(36-АО в квадрате), треугольникАОН, уголОАН=60/2=30, АО=2*ОН
ОН*2*корень11 = корень(36-4*ОН в квадрате), две части в квадрат
44*ОН в квадрате=36 - 4*ОН в квадрате, 48*ОН в квадрате=36, ОН=корень3/2
ВН=ОН*3=корень3*3/2=3*корень3/2, АС=2*ВН*корень3/3 = 2*корень3*корень3/3*2=1
Стороны прямоугольника (х-8) см и 2х см, площадь (х-8)·2х
По условию площадь прямоугольника равна площади квадрата, составляем уравнение
х²=(х-8)·2х
х²=2х²-16х
х²-16х=0
х(х-16)=0
х=0 или х-16=0
х=16
Стороны прямоугольника
(х-8)=16-8=8 см
и
2х=2·16=32 см
ответ. 8 см; 32 см