Вариант решения.
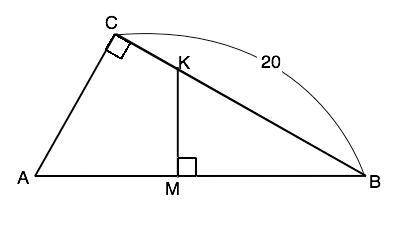
Пусть в треугольнике АВС ∠С=90°, В - вершина меньшего острого угла, а КМ – перпендикуляр к гипотенузе. Расстояние от точки до прямой равно длине перпендикуляра между ними. Искомый отрезок - ВМ.
Δ АВС подобен Δ КВМ по общему острому углу СВА.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
По условию Ѕ(АСВ):Ѕ(КВМ)=2, и это отношение равно k² . ⇒ k=√2, следовательно, ВС:BM=√2 ⇒ MB=BC:√2=20:√2=10√2 см
квадрат.
Объяснение:
Думаю, что задание звучало по-другому:
"Начертить четырёхугольник, у которого есть минимум 3 прямых угла, и две последовательные стороны имеют одинаковую длину"
Если это так, то рассуждаем следующим образом.
1. Сумма углов четырёхугольника равна 360°. Три из них по условию в сумме дали 270°, тогда и третий равен 90°, речь в задаче по определению идёт о прямоугольнике.
2. Смежные ( соседние, имеющие общую вершину) стороны этого прямоугольника, которые при изображении откладывают последовательно друг за другом, равные. Противолежащие стороны прямоугольника равны по свойству, тогда все стороны получатся равными, данный прямоугольник является квадратом.
ответ: необходимо начертить квадрат.
проще всего, наверное, через площадь решать...
площадь прямоугольного треугольника = половине произведения катетов...
площадь любого треугольника (в том числе и прямоугольного) = половине произведения двух сторон на синус угла между ними...
расстояние от точки до прямой--это перпендикуляр))