Пусть R, r -- радиусы двух окружностей, O₁, O₂ -- их центры.
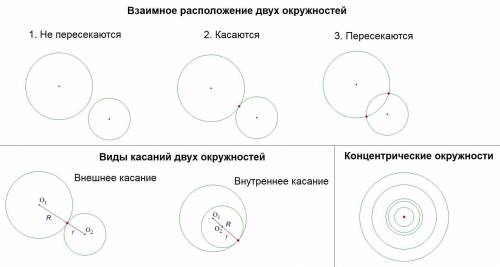
1. Взаимное расположение двух окружностей
Выделяют три основных случая взаимного расположения окружностей:
Две окружности не имеют общих точек (не пересекаются)Две окружности имеют одну общую точку (касаются)Две окружности имеют две общие точки (пересекаются)Также выделяют иногда четвёртый случай: совпадающие окружности (бесконечное множество общих точек).
2. В каком случае окружности имеют одну общую точку?
Окружности будут иметь одну общую точку, если:
Сумма их радиусов равна расстоянию между центрами (R + r = O₁O₂).Разность их радиусов равна расстоянию между центрами (R - r = O₁O₂).3. Как называется общая точка двух окружностей?
Если окружности касаются в некоторой точке, то такая точка называется точкой касания.
Если пересекаются -- точкой пересечения.
4. Виды касаний двух окружностей
В пункте 2 было выделено два признака касания окружностей, откуда получается 2 вида касания:
Внешнее касание (R + r = O₁O₂)Внутреннее касание (R - r = O₁O₂)5. Когда окружности пересекаются?
Окружности пересекаются, когда расстояние между центрами меньше суммы радиусов, но больше их разности: R - r < O₁O₂ < R + r
6. Концентрические окружности
Окружности, имеющие общий центр, называются концентрическими.
Тогда ∠BOC=2∠BAC=50°=∠BDC.
Значит D лежит на окружности, описанной около треугольника BOC.
Аналогично, ∠BOA=2∠BCA=100°=∠BDA.
Значит D лежит на окружности, описанной около треугольника BOA,
а значит D - одна из двух точек пересечения этих окружностей, которые есть О и B. Очевидно, что D совпадать с B не может, значит D совпадает с О. Т.е. D - центр окружности, описанной около ABC. Отсюда BDC - равнобедренный, ∠DBC=(180°-50°)/2=65° и значит угол между диагоналями ABCD равен 180°-∠DBC-∠BCA=180°-65°-50°=65°.