Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =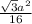 
(кв.ед.)
Из формулы площади шестиугольника S=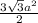
выражаем сторону а:
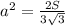
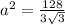
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
1))) обозначим сторону 6-угольника АВ, О---центр
в треугольнике АОВ угол АОВ = 360/n = 360/6 = 60, т.е. 6-угольник разбивается на 6 правильных треугольников и S(6-угольника) = 6*S(АОВ)
S(АОВ) = АВ*(r) / 2, где высота = r вписанной окружности
осталось найти сторону 6-угольника, зная радиус вписанной окружности...
если радиус вписанной в n-угольник окружности через сторону выражается:
r = a / (2*tg(180/n)), то a = r * 2*tg(180/n)
АВ = r * 2*tg(180/6) = r * 2*tg(30) = r *2*корень(3) / 3
r = d / 2, где d ---диагональ вписанного в окружность квадрата
по т.Пифагора d^2 = 2a^2, где а---сторона квадрата
d = a*корень(2)
r = d/2 = a*корень(2) / 2
S(АОВ) = АВ*r / 2 = (r *2*корень(3) / 3) * r / 2 = r^2 * корень(3) / 3 = a^2 * корень(3) / 6
S(6-угольника) = a^2 * корень(3)
S = ( )^2 * корнеь(3) = корень(12)*корень(3) = корень(36) = 6
Круг можно тремя разрезами разделить на 7 частей: Линия каждого разреза пересекается с двумя другими и получится 3•2 части, плюс часть, которая получится между ними (см. рисунок).
Блин также можно разделить на 7 частей, если его не сворачивать. Если первым разрезом поделить блин пополам, затем наложить одну половину на другую и двумя сквозными пересекающимися разрезами разделить эти половини еще на 4 части , то блин можно разделить на 8 частей.
Так как каравай имеет высоту, можно разделить его таким образом:
Первый разрез провести по высоте - получатся две круглые части.
Затем крестообразно провести еще два разреза от края до края и получить наибольшее количество частей, на которое его можно разделить - 8 частей.