Дано:
тр. АВС - равнобедр.
КМ = 5 см
Р(перимитр)тр.АВС = 32 см
Найти: АВ, ВС, СА
КМ || ВС
КМ = 1/2 ВС
ВС = 5*2=10 см
АВ = ВС = 10 см (т.к. треуг. равнобедр.)
АС = 32 - (10+10) =12 см
ответ: АВ = 10 см; ВС = 10 см; АС = 12 см
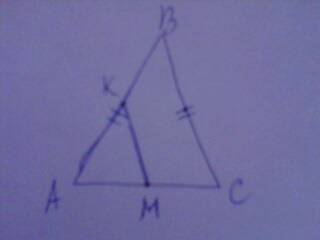
Дано: АВСД-квадрат, АС и ВД-диагонали, О-точка пересечения АС и ВД
Найти: Р(АВСД)-?
Кратчайшее расстояние от точки до прямой-это перпендикуляр, опущенный из данной точки на данную прямую.
Опустим ОН-перпендикуляр к АВ. По условию, ОН=5 см.
СВ-перпендикулярно АВ (т.к. АВСД-квадрат), ОН-перпендикулярно АВ
Следовательно, ОН II CВ.
Треугольник ОНВ - прямоугольный, в нём углы ОВН = ВОН = 45 град,
значит ОНВ-равнобедренный, ВН=ОН=5 (см)
Аналогично, АН=ОН=5(см)
АВ=АО+ВО=5+5=10(см)
Находим периметр: Р(АВСД)=4АВ=4*10=40(см)
ответ: 40 см
Обьяснение:
они равны по 1 признаку равенства треугольников, ac=bc, угол bco=aco, co-общая сторона, 2 признак: если провести прямую от b до a, то получится, что abc- равнобедренный, соответственно, равны углы cba и cab, доказательство: угол cba =cab, AC=bc, угол ocb=oca, 3 признак: по 2 признаку мы провели прямую от а до b, и получили, что abc- р/б, проведя прямую ОС до прямой Ab получим, что она будет являться и медийной и высотой и биссектрисой(это признак или свойство), следовательно, ао=Bo, доказательство: AC=Bc, oc- общая, АО =Bo.
средняя линия треугольника = 1/2 от основания. Значит нижнее основание = 10. Раз треугольник равнобедренный, то все стороны по 10.
проверим Р=2(10+10+10)=32