Вот еще - о пользе знакомства с Пифагором :)
Высота делит треугольник на два прямоугольных треугольника с катетами 9, 12 и 12, 16.
Легко видеть, что оба эти треугольника "египетские", то есть подобные треугольнику со сторонами 3, 4, 5. Так же и ВЕСЬ треугольник тоже будет "египетским", со сторонами 15, 20, 25.
Угол напротив стороны 9 + 16 = 25, само собой - прямой, и сторона эта - гипотенуза.
Медиана делит гипотенузу пополам, на отрезки 12,5.
Биссектриса прямого угла делит гипотенузу на отрезки в отношении 15/20 = 3/4, то есть отрезок, имеющий общую вершину с меньшим катетом, будет 25*3/(3+4) = 75/7, а второй отрезок 100/7. (Проверьте, в сумме 25, и отношение 3/4)
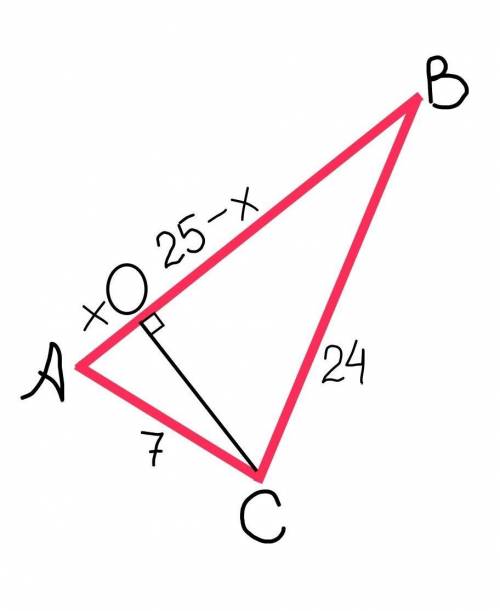
Дано:
АС=7 см;
АВ=25 см;
ВС=24 см.
СО – высота, проведенная к АВ.
Высота, пересекаясь со стороной, к которой проведена, образует прямой угол.
То есть угол ВОС=90° и угол АОС=90°.
Следовательно ∆ВОС – прямоугольный с прямым углом ВОС и ∆АОС – прямоугольный с прямым углом АОС.
Пусть АО=х, тогда ВО=АВ–АО=25–х.
По теореме Пифагора в прямоугольном треугольнике ВОС:
ВС²=ВО²+СО²
СО²=ВС²–ВО²
СО²=24²–(25–х)²
СО²=576–625+50х–х²)
СО²=–х²+50х–49 (Ур 2)
По теореме Пифагора в прямоугольном треугольнике АОС:
АС²=АО²+СО²
СО²=АС²–АО²
СО²=7²–х²
СО²=49–х² (Ур 2)
Тогда можем составить уравнение, объединив Ур 1 и Ур 2, получим:
–х²+50х–49=49–х²
50х=98
х=1,96
Тоесть АО=1,96 см.
Подставим значение АО и известное значение АС в уравнение СО²=АС²–АО², получим:
СО²=49–3,8416
СО²=45,1584
СО=6,72 см.
ответ: 6,72 см.
надо все плюсовать
+ + + + ++ + + +