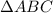
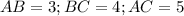
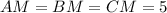
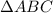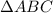. . Это - египетский прямоугольный треугольник, что подтверждается теоремой Пифагора: 
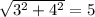. А центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы. Итак, радиус этой окружности равен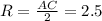 
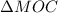. В нем 
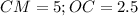. Третью сторону найдем по теореме Пифагора: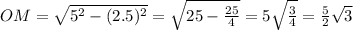
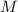до плоскости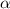 
SAB - данное сечение, ∪АВ = α.
Пусть Н - середина АВ, тогда ОН⊥АВ, так как ΔАОВ равнобедренный (АО = ОВ как радиусы), SH⊥АВ, так как ΔSAB равнобедренный (SA = SB как образующие), ⇒ ∠SHO = φ - линейный угол двугранного угла наклона сечения к плоскости основания.
ΔSOH: ∠SOH = 90°, ctgφ = OH / h
OH = h·ctgφ
ОН - медиана, высота и биссектриса ΔАОВ, ⇒ ∠АОН = α/2.
ΔАОН: ∠AHO = 90°,
cosα/2 = OH/AO, ⇒ R = AO = OH / cosα/2
R = h·ctgφ / cosα/2
V = 1/3 πR²h = 1/3 · π · h · (h·ctgφ / cosα/2)²
V = πh³·ctg²φ / (3cos²α/2)
Sбок=P*H, Sбок=4*6*12=288
Sосн=a², Sосн=6²=36
Sп.п=288+2*36
Sп.п=360 см²