Начнём с вычисления градусных мер нужных нам дуг.
Угол ВАС = 30⁰ равен половине градусной меры дуги на которую он опирается, значит дуга ВС=60⁰.
Угол ВОС = 60⁰, как центральный угол, опирающийся на дугу ВС, а углы АОВ и АОС равны (360-60)/2=150⁰, поскольку АВ=ВС.
Теперь переходим к выражению площадей:
Площадь всего круга:
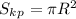
Площадь одного из заштрихованных сегментов:
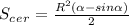 , где α- градусная мера дуги сегмента в радианах (150⁰=5π/6)
, где α- градусная мера дуги сегмента в радианах (150⁰=5π/6)
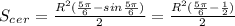
Площадь интересующей нас фигуры (на рисунке- красным цветом) есть разность между площадью всего круга и двух сегментов (штриховка):
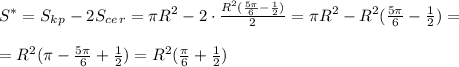
Таким образом отношение площади той части круга, которая заключена в этом угле (на рисунке- красным), к площади всего круга будет равно:

Ну и, если всё правильно, как "Лучшее решение" не забудь отметить, ОК?!... ;)))
sin2 α + cos2 α = 1.
в основном это ищеться через теорему пифагора
надо 4 треугольника одинаковых прямоугольных, с единичной гипотенузой, и поставить их так, чтобы их катеты образовали квадрат, и гипотенузы тоже образовали квадрат: теперь рассматриваем площади: площадь малого квадрата 1, возьмём произвольный острый угол в прямоугольном треугольнике, тогда по определению один из катетов синус, а второй косинус:
считаем площади: площадь большого квадрата (sinx + cosx)^2 = 1 + 4* 1/2 sinx*cosx
дальше раскрываем скобки, взаимно уничтожаем удвоенные произведения синуса на косинус и получаем наше тождество
Найдите косинус угла AKC, если ∠KAC>90°
---------
Треугольник АВС тупоугольный (АС²>АВ²+ВС²); против большего угла лежит большая сторона.
АС-большая сторона.⇒∠ В>90º.
Т.к. по условию ∠ КАС>90º, а ∆ АКС ~ ∆ АВС, ∠КАС=∠В.
Тогда, поскольку треугольники подобны,
∠ КАС >90º, КС - большая сторона ∆ АКС.
∠АКС=∠ВСА
По т.косинусов
АВ²=АС²+ВС² -2 АС*ВС*cos∠ACB ⇒
cos∠ACB=(АВ²-АС²-ВС²)/( -2АС*ВС)
cos∠ACB=6/(-6√2)=1/√2=(√2)/2⇒
cos∠АКС=(√2)/2 - это косинус угла=45º