Snlm=6 кв.см.
Объяснение:
Дано:
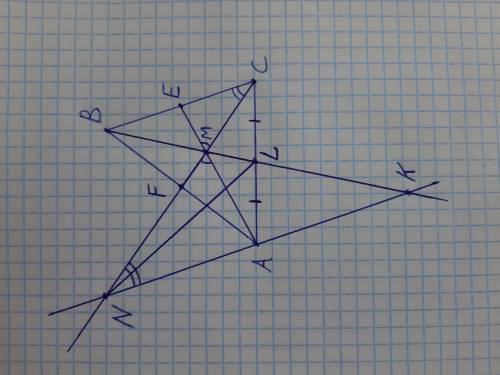
ΔABC; Sabc=18 кв.см.
M-точка пересечения его медиан.
AE;BL;CF-медианы.
MK║BC
Найти: Snlm-?
1) LEMC=LNMA - по свойству вертикальных углов.
2) LCNA=LNCB - накрест лежащие углы.
3) ΔCME и ΔAMN - подобные по двум углам (первый признак подобия)
4) По свойствам медианы:
Safm=Sfbm=Sbem=Semc=Smlc=Smal⇒Semc=Sabc/6=18/6=3 кв.см.
5) По свойствам медианы: AM/ME=2/1=2
Так как AM и ME подобные стороны ΔCME и ΔAMN, то коэффициент подобия k=AM/ME=2
6) Зная коэффициент подобия, вычислим Samn:
Samn=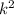
*Scme=
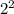*3=4*3=12 кв.см.
7) Sanc=Sanm+Saml+Slmc=12+3+3=18 кв.см.
8) Медиана-NL делит площадь в ΔANC на две равновеликие части поэтому:
Slnc=Sanc/2=18/2=9 кв.см.
9) Искомая площадь ΔNLM равна:
Snlm=Slnc-Slmc=9-3=6 кв.см.
Уравнение окружности: (х - х₀)² + (у - у₀)² = R², где О(x₀; y₀) - центр окружности; R - радиус окружности.
Так как МК - диаметр данной окружности ⇒ О (центр окружности) - середина МК.
х₀ = (М(х) + К(х))/2 = (-3 + 5)/2 = 1.
у₀ = (М(у) + К(у))/2 = (4 + 10)/2 = 7.
⇒ O(1;7)
OM = OK - радиусы данной окружности.
MK - диаметр, по условию.
МК = √((K(x) - M(x))² + (K(y) - M(y))²) = √((5 - (-3))² + (10 - 4)²) = √(64 + 36) = 10.
⇒ OM = OK = MK/2 = 10/2 = 5.
Итак, уравнение данной окружности:
(х - 1)² + (у - 7)² = 25.
Теперь, с уравнения данной окружности, найдём а:
Р(-10;а)
х = -10.
у = а.
(-10 - 1)² + (а - 7)² = 25
(-11)² + а² - 14х + 49 = 25
121 + а² - 14х + 49 = 25
170 + а² - 14х - 25 = 0
145 + а² - 14х = 0
а = -(-14) ±√(((-14)² - 4 * 1 * 145)/2 * 1
а = 14 ±√(-384)/2
а ∉ R. (а не является элементом множества R)
R - любое, положительное или отрицательное число.
ответ: а ∉ R.
1)Медианы треугольника пересекаются в одной точке вне треугольника - неверно
2)Высота, проведенная из вершины угла к гипотенузе, является средним пропорциональным между катетами прямоугольного треугольника - неверно
3)Площадь трапеции равна произведению полусуммы оснований на высоту -верно
Неверное: 1,2
II
1)Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам - Верно
2)Отношение площадей подобных треугольников равно коэффициенту подобия - неверно
3)Гипотенуза прямоугольного треугольника меньше катета - неверно
Верно: 1
III
1)Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2:1 , считая от вершины - верно
2)Высота, проведенная из вершины прямого угла на гипотенузу, делит гипотенузу на две равные части - неверно.
3)Площадь трапеции равна произведению полусуммы оснований на высоту - верно
Неверно: 2