ответ: 24 см
Объяснение:
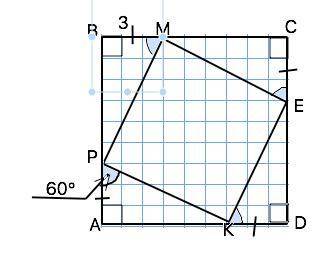
Так как все стороны квадрата равны, а отрезки AP=BM=CE=DK=3, то и РВ=МЕ=ЕD=АК, ( если от равных величин отнять по равной части, оставшиеся части также равны). ⇒ Прямоугольные треугольники, образовавшиеся при углах квадрата, равны по двум катетам.
Сумма острых углов прямоугольного треугольника равна 90°⇒
В⊿ АРК угол РКА=90°- 60°=30°
Катет АР=3 см и противолежит углу 30°⇒
Гипотенуза РК=2•АР=2•3=6 см
Сходственные стороны равных треугольников равны. Таких треугольников 4, гипотенуза каждого 6 см и является стороной четырехугольника PMEK, поэтому периметр
РМЕК=4•6=24 см
1) Боковая поверхность правильной пирамиды состоит из трех равнобедоенных треугольников с боковой стороной 8 см (по условию) и углам при вершине 60 градусов. Значит, углы при основании в этих тр-ках равны по (180-60)/2=60 градусов, т.е. как в основании, так и в боковых гранях лежат правильные равные треугольники со стороной 8 см.
2) Площадь боковой поверхности такой пирамиды равна сумме площадей трех равносторонних тр-ков. Площадь правильного тр-ка равна ((a^2)*sqrt(3))/4=
=(64*sqrt(3))/4=16*sqrt(3). А площадь боковой поверхности равна 3*16*sqrt(3)=
=48*sqrt(3) (см^2)