Написала на картинке.
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания.Сумма периметров треугольников АВС и DEF равна 16 см (7 см+9 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 16 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 16 см
PK+KL+LM+MN+NR+PR < 8 см.
Это нам и нужно было доказать!



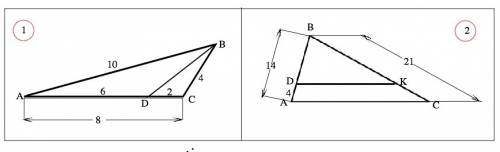
1) DC=AC-AD=8-6=2 см. Угол С общий для треугольников АВС и DВС, стороны, содержащие этот угол, пропорциональны (АС:ВС=ВС:DC=2). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Из подобия следует АВ:ВD=2, ⇒ BD=10:2=5 см
———————————
2) Обозначим К точку пересечения прямой из т.D с ВС. По условию DK||АС, тогда стороны АВ и ВС треугольника являются секущими для них. ⇒ соответственные углы при DK и АС равны, треугольники АВС и DBK подобны по равным углам. Из подобия следует АВ:DB=ВC:ВK. ВD=AB-AD=10. ⇒ 14:10=21:ВК ⇒ ВК=210:14=15 см. Поэтому КС=21-15=6 см. Сторона ВС делится на отрезки 15 см и 6 см.
Обозначим центры окружностей К и М, а точку пересечения АВ и прямой КМ - Н.
Боковые стороны ∆ АКВ - радиусы, ⇒ ∆ АКВ - равнобедренный.⇒
∠КАВ=∠ КВА
Боковые стороны ∆ АМВ радиусы, ⇒ ∆ АМВ равнобедренный. ⇒
∠МАВ=∠МВА
В треугольниках КАМ и КВМ углы при А и В - сумма равных углов. ⇒
∠КАМ=∠КВМ
стороны КА=КВ, АМ=ВМ⇒
∆ КАМ=∆КВМ по двум сторонам и углу между ними. ⇒
∠АКН=∠ВКН, и ∆ АКН=∆ ВКН. ⇒
АН=ВН, и тогда КН - медиана равнобедренного ∆ АКВ, и его биссектриса и высота. ⇒
КН⊥АВ, что и требовалось доказать.