ответ: 150º
Объяснение:
Отрезки ОА и ОВ - радиусы окружности. Расстояние от точки А до прямой ОВ в два раза меньше радиуса. Найдите дугу АВ.
Вариант а) рис.1
Точка А расположена в той же четверти окружности, что В.
Расстояние от точки до прямой - перпендикуляр. Пусть это перпендикуляр АС.
В прямоугольном треугольнике АОС отрезок АС=0,5 АО. Синус угла АОС=АС:АО=0,5. Это синус угла 30º
Центральный угол окружности равен угловой величине дуги, на которую он опирается. ⇒ дуга АВ=30º
Вариант б) рис.2
Точка А расположена по другую сторону от центра, чем В.
Тогда точно так же найдем величину угла между радиусом ОА и прямой ОВ. Дуга АВ в этом случае равна разности межу развернутым углом ВОС и углом АОС.
дуга АВ=180º-30º=150º
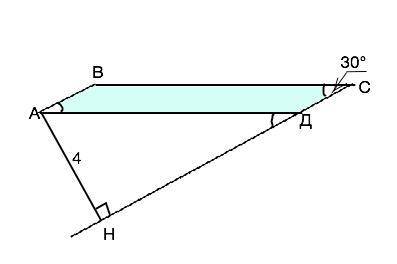
ответ: 1 см; 8 см; 1 см; 8 см. Два угла по 30°, два других по 150°
Объяснение: В параллелограмме противоположные углы равны. => угол А=угол С=30°. Сумма углов четырехугольника (а параллелограмм - четырехугольник) равна 360°. ⇒ ∠В=∠Д=(360°-2•30°):2=150°
ВС║АВ, прямая СД - секущая ⇒ соответственные ∠ВСД=∠АДН.
В прямоугольном ∆ АДН катет АН противолежит углу 30°, следовательно, гипотенуза АД=2•АН=2•4=8 см (свойство).
В параллелограмме противоположные стороны равны. ВС=АД=8 см.
Р=18=2АВ+2АД ⇒2АВ=18-16=2 ⇒ АВ=СД=2:2=1 (см)
угол АДВ=углу ДВС( накрест лежащие при параллельных ВС и АД и секущей ВД); углы АВД, ДВС и СДВ равны, т.к. ВД - биссектриса; отсюда тр-к ВСД равнобедренный; ВС=СД=25 см;
опустим высоту СН на АД; ВС=АН=25см; отсюда ДН=32-25=7 см;
в тр-ке СНД по т. Пифагора СД^2=CH^2+HD^2, CH^2=625-49=576,
СН=24 см - это высота трапеции;
S=(а+в)/2*h=(25+32)/2*24=684 см кв. - это ответ.