ответ: Не верьте громоздким готовым формулам, они отучают думать
Объяснение:
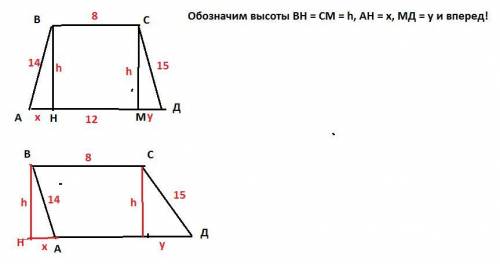
Трапеции бывают разные. Вот если мы применим рисунок со стандартной трапецией, то выяснится, что она не существует.
неизвестная будет отрицательная и прочие неприятности. Но на втором рисунке тоже трапеция, так как АД||ВС, а две другие стороны не параллельны. Вот его мы и решим.
Когда мы провели две высоты мы от основания отрезали отрезок
что у = АД - 8+х или у=4+х Это первое уравнение.
Из прямоугольных треугольников на рисунке выразим высоту, не спеша вдумчиво и применяя теорему святого Пифагора:
Из ВНА будет h² = AB² - x²
Из СМД будет h² = CД² - у² и так как левые части равны, приравняем и правые части АВ²-х² = СД² -у² или подставив значения боковых сторон 14²-х² = 15²-у² а отсюда уже
у²-x²=225-196 = 29 уравнение. Решив систему этих уравнений (я расписывать это здесь не буду, нудно) мы получим, что х=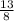
Тогда из треугольника ВНС
h² = 14² -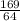 
= 13,9
И это решение верное.
1. Дано: КМРТ - трапеция, КМ=РТ, КТ=14 дм, МР=8 дм. МН - высота, МН=4 дм. Найти КМ.
Решение: проведем высоту РС.
МР=СН=8 дм.
ΔКМН=ΔРСТ по катету и гипотенузе, КН=СТ=(14-8):2=3 дм.
Рассмотрим ΔКМН - прямоугольный, КН=3 дм, МН=4 дм, значит КМ=5 дм (египетский треугольник).
ответ: 5 дм.
2. Дано: КМСТ - прямоугольник, Р=56 см, КТ-МК=4 см. Найти МТ.
Решение: МК+КТ=56:2=28 см. Пусть КТ=х см, тогда МК=х-4 см.
Составим уравнение: х+х-4=28; 2х=32; х=16.
КТ=16 см; МК=16-4=12 см. Тогда по теореме Пифагора
МТ=√(16²+12²)=√(256+144)=√400=20 см.
(или просто: МТ=20 см, т.к. МК:КТ=12:16=3:4; МКТ - египетский треугольник)
ответ: 20 см.