..................................................................

Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.
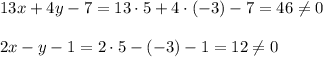
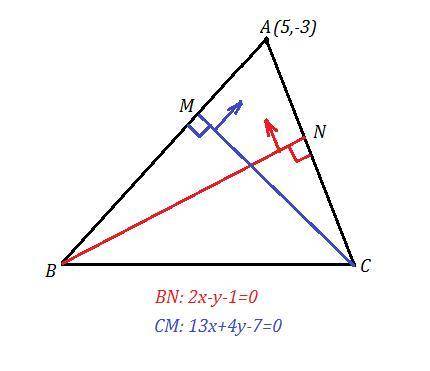
Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.
BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN:  .
.
Точка А(5,-3)∈АС и уравнение АС имеет вид:
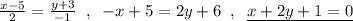
CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ:  .
.
Точка А(5,-3)∈АВ и уравнение АВ имеет вид:
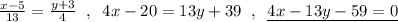
Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .
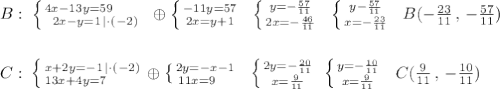
АВСД- трапеция, МТ перпендикуляр к АД. S=½KD·MT, МТ- средняя линия ΔДВК,
МТ=½ВК =½·1=½, КД=КО+ОД ( СО -перпендикуляр к АД) .ΔАВК=ΔСОД,
ОД=АК;ΔАВК, <К=90⁰,ВК=½АВ(как катет,что лежит против угла в 30⁰), откуда АВ=2·ВК=2·1=2 , по т. Пифагора АК=
=√(АВ²-ВК²)=√(4-1)=√3. КД=2+√3. S=½ (2+√3)·½=(2+√3)/4
ответ: (2+√3)/4см²