Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
1) M - cередина AD, M∈(ABC), C∈(ABC) ⇒ проведем MC (B1C)∈(BCC1), M∈(ADD1), а т.к. (ADD1) || (BCC1), то секущая плоскость будет пересекать (АDD1) по прямой k, проходящей через точку М параллельно B1C. k пересечет АА1 в точке N, причем AN=NA1. N∈(AA1B1) и B1∈(AA1B1) ⇒ проведем NB1 MNB1C - сечение куба 2) MN || B1C, CM=B1N=√(a²-(a/2)²)=a√3/2 ⇒ MNB1C трапеция S (MNB1C) = 1/2 (MN+B1C) * NH, где NH - это высота трапеции B1C=a√2 / 2 MN = 1/2 B1C = a√2 / 4 B1H = 1/2 (B1C - MN) = a√2 / 4 NH = √(B1N² - B1H²) = a√10 / 4 S (MNB1C) = 3 a² √5 / 16
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их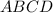
и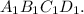 
Проведём диагональ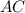
в квадрате 
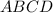и диагональ 
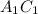в квадрате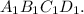 
Рассмотрим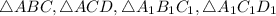
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.